Discrete And Continuous Values Of Images: Understanding The Difference

Discrete and Continuous Values of Images

Images are a fundamental part of our visual world, and understanding the different types of values they can possess is crucial in various fields, including image processing, computer vision, and machine learning. Two main types of values that images can have are discrete and continuous. In this article, we will delve into the definitions, attributes, examples, properties, relationships, applications, and advantages/disadvantages of discrete and continuous values of images.

Definition and Overview:

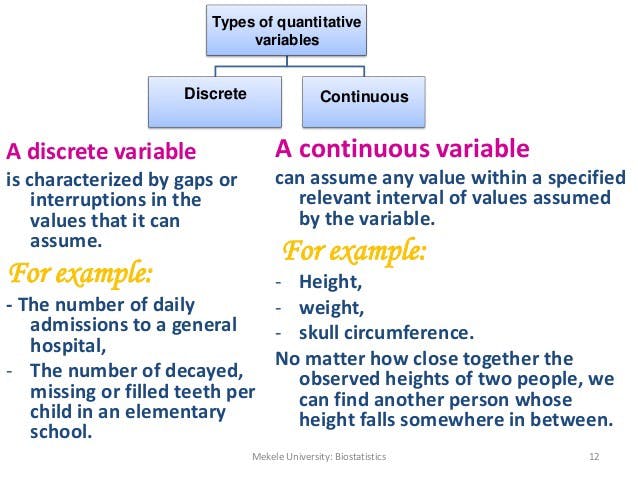
Discrete values refer to values that have a finite or countable number of possibilities. In the context of images, discrete values are characterized by their limited and enumerable nature. On the other hand, continuous values have an infinite range of possibilities and are not countable or enumerable. Continuous values in images are associated with smooth or gradual variations.

Attributes of Discrete Values:

1. Limited values: Discrete values in images are restricted to a finite or countable set of options. For example, in binary images, pixels can only have two values – black or white.

2. Discrete intervals: The space between discrete values is non-continuous and can consist of specific intervals or steps. For instance, the color palette of an image may have discrete values that represent different shades or colors.

3. Countable and enumerable: Discrete values are countable in that they can be measured or enumerated distinctly. Each value can be assigned a unique count or identifier.

4. Non-continuous: Discrete values do not exhibit a continuous transition between different options. There is no intermediate state between each discrete value.

Examples of Discrete Values in Images:

1. Pixel values: Each pixel in a digital image is characterized by a discrete value. This value determines the intensity or color of the pixel.

2. Color palette: Certain images, such as indexed color images, use a discrete set of pre-defined colors from a fixed color palette. Each pixel in the image is associated with one of these discrete colors.

3. Binary images: Binary images consist of pixels that can only take two discrete values, typically representing black and white areas.

4. Grayscale images: Grayscale images use pixel values ranging from 0 to 255 to represent different shades of gray. Each value represents a discrete shade.

Properties of Continuous Values:

1. Infinite possibilities: Continuous values have an infinite range of possibilities. There is no limit to the number of potential values that can exist between any two points.

2. Continuous intervals: The space between continuous values is a continuous interval. Any value within this interval is considered valid and can exist in the image.

3. Non-countable and non-enumerable: Continuous values are not countable or enumerable due to their infinite nature. It is impossible to distinctly measure or assign a unique count to each possible value.

4. Continuous variation: Continuous values exhibit smooth and gradual variations. There are no sudden jumps or steps between different values.

Examples of Continuous Values in Images:

1. Color intensity: Continuous values can represent the intensity or brightness of colors in an image. These values can vary continuously, allowing for a wide range of shades and hues.

2. Smooth gradients: Images can contain smooth gradients where the values transition gradually from one color to another. These gradients are made possible by continuous values.

3. Analog images: Analog images, such as photographs captured on film, often possess continuous values. The variations in color and intensity are not limited to discrete values.

4. Gradient fields: Continuous values can be used to represent gradient fields in images. These fields indicate the direction and magnitude of color or intensity changes across the image.

Relationship between Discrete and Continuous Values in Images:

1. Conversion between discrete and continuous representations: Images can be converted between discrete and continuous representations through suitable algorithms. This conversion allows for different operations and analyses on the image data.

2. Sampling and quantization processes: During the acquisition or digitization of an image, continuous values are converted into discrete values through sampling and quantization processes. These processes involve measuring the continuous values at discrete points and representing them with discrete values.

3. Role of resolution in determining continuity or discreteness: The resolution of an image, which determines the level of detail captured, can impact its continuity or discreteness. Higher resolution images tend to exhibit more continuous variations, while lower resolution images may have more stepped or blocky appearances.

4. Impact on image quality and perception: The presence of discrete or continuous values affects image quality and perception. Discrete values can result in visible pixelation or artifacts, while continuous values allow for smoother and more realistic representations.

Applications of Discrete and Continuous Values in Image Processing:

1. Digital image compression techniques: Both discrete and continuous values play a vital role in image compression algorithms. Discrete values can be efficiently compressed by identifying patterns and redundancies, while continuous values contribute to preserving image quality during compression.

2. Image enhancement and manipulation algorithms: Image enhancement and manipulation techniques often operate on both discrete and continuous values. These algorithms can enhance or modify specific features based on the characteristics of the image values.

3. Digital signal processing methods: Digital signal processing methods use both discrete and continuous values to analyze and manipulate image data. Techniques such as filtering, noise reduction, and feature extraction rely on the properties of these values.

4. Machine learning and computer vision applications: Discrete and continuous values are essential in machine learning and computer vision applications. Algorithms that rely on image data, such as object detection or image recognition, leverage these values to make accurate predictions and classifications.

Advantages and Disadvantages of Discrete and Continuous Values in Image Processing:

1. Advantages of discrete values: Discrete values allow for precise and efficient representation of certain image types, such as binary images. They simplify computations and can be easily processed by algorithms designed for specific discrete values.

2. Advantages of continuous values: Continuous values provide a more natural and realistic representation of images, enabling smoother transitions between colors or intensities. They can convey subtle details and contribute to enhanced image quality.

3. Limitations of discrete values: Discrete values have limitations in terms of representing complex or continuous variations. They may result in loss of information and visible quantization artifacts when applied to images that require smooth gradients.

4. Limitations of continuous values: Continuous values can consume more storage space and computational resources compared to discrete values. Processing continuous values may also be more complex, as algorithms need to handle infinite possibilities.

Conclusion and Future Developments:

Understanding the concepts of discrete and continuous values in images is crucial for various image processing applications and analyses. Discrete values provide a practical and efficient representation for specific image types, while continuous values allow for more realistic and precise representations. Advances in image processing techniques aim to minimize the limitations associated with both types of values, ultimately leading to improved image quality, perception, and analysis in the future.

FAQs:

Q: What is a continuous image?
A: A continuous image refers to an image that possesses continuous values, allowing for smooth variations and transitions between colors or intensities.

Q: What is continuous image math?
A: Continuous image math involves mathematical operations and calculations applied to images that have continuous values. These operations utilize the properties of continuous values to process and analyze images.

Q: What are discrete values of an image?
A: Discrete values of an image refer to values that have a finite or countable number of possibilities. These values are limited, enumerable, and non-continuous.

Q: How do discrete and continuous values relate to image quality?
A: Discrete values can result in visible artifacts and pixelation, impacting image quality. On the other hand, continuous values allow for smoother and more realistic representations, contributing to enhanced image quality.

Q: Can an image have both discrete and continuous values?
A: Yes, an image can have both discrete and continuous values. Certain attributes or components of the image may possess discrete values, while others exhibit continuous variations. The coexistence of both types of values allows for a more comprehensive representation of the image.

Is An Image Discrete or Continuous?

When we think about images, we often visualize photographs, paintings, or any visual representation that captures a scene, person, or object. But have you ever wondered whether an image is discreet or continuous? The question may sound trivial, but it has profound implications in fields such as computer science, mathematics, and even our daily lives. In this article, we will delve into the characteristics of images, explore the concepts of discreteness and continuity, and understand how they apply to the world of images.

Before delving into the nature of images, let us first explore the definitions of discreteness and continuity. In mathematics, discreteness refers to a set of values that are separate and distinct, with no intermediary elements. On the other hand, continuity describes a set of values that are connected and have no gaps or jumps. These concepts can be better understood by considering natural numbers as an example. The set of natural numbers, such as 1, 2, 3, 4, 5…, is discrete because there are no intermediary numbers between them. In contrast, the set of real numbers, which includes both whole numbers and decimals like 1.5, 2.7, and so on, is continuous as there are infinite possible values between any two numbers.

Now, let’s apply these concepts to images. An image consists of pixels, which are tiny dots that make up the image. Each pixel holds a specific color or grayscale value, representing the intensity of light at that particular point. When we zoom in on a digital image, we can observe individual pixels that form a grid-like pattern. This discrete nature of pixels, with each pixel having its own value, suggests that an image is discrete in nature.

However, despite its discrete representation at the pixel level, an image can be seen as a continuous entity when viewed as a whole. Think of an image like a painting. When we look at a painting from afar, it appears smooth, with no obvious signs of individual brushstrokes. Similarly, when we view an image on a screen, we see a coherent picture that appears continuous to our eyes. This illusion of continuity is achieved by various techniques such as interpolation and anti-aliasing, which smooth out the transitions between pixels, making the image appear seamless.

The digital world has made significant progress in bridging the gap between discreteness and continuity. Consider vector graphics, which are based on mathematical equations rather than a grid of pixels. Vector graphics use curves, lines, and shapes to describe an image instead of relying on individual pixels. As a result, vector images can be scaled to any size without losing quality, as the mathematical equations can adjust the shapes accordingly. Vector graphics offer the advantage of easy editing and manipulation, as they are not limited by the fixed resolution of pixel-based images.

Now, let’s address some frequently asked questions to further clarify the discreteness and continuity of images:

Q: Are photographs discrete or continuous?
A: Photographs, as pixel-based images, can be considered discrete due to the presence of individual pixels. However, when viewed as a whole, photographs create an illusion of continuity to our eyes.

Q: What about analog images, such as film photography?
A: Analog images, such as film photographs, are continuous in nature. Unlike digital images, which are composed of pixels, analog images record information on a continuous medium, such as film or photographic paper.

Q: Can an image be both discrete and continuous?
A: It may seem contradictory, but an image can possess both discrete and continuous qualities simultaneously. At the pixel level, an image is composed of individual elements, making it discrete. However, when we perceive the image as a whole, it appears continuous.

Q: How does the distinction between discreteness and continuity impact image processing?
A: Understanding the nature of images helps in image processing tasks such as resizing, compression, and filtering. Techniques like interpolation and anti-aliasing help maintain the illusion of continuity while manipulating images.

In conclusion, the question of whether an image is discrete or continuous may seem simple, but it encompasses complex concepts. While images are composed of individual pixels and have a discrete representation at the pixel level, they can appear continuous when viewed as a whole. Understanding the discreteness and continuity of images allows us to appreciate their beauty, analyze their characteristics, and develop effective image processing algorithms.

What is a Discrete Image?

In the world of digital imaging and computer vision, a discrete image is a representation of visual information that is divided into distinct, well-defined elements. These elements, called pixels, make up the image in a structured, grid-like format. Each pixel represents a specific location and contains a discrete value that describes the color, brightness, or other visual attributes of that location. Discrete images are the foundation of many modern technologies, ranging from digital photography and graphic design to medical imaging and autonomous vehicles.

The Concept of Discrete Images

The concept of a discrete image is closely related to the field of digital signal processing. In digital imaging, a continuous visual scene is sampled at regular intervals to create a discrete representation. This discrete representation, which consists of a finite number of pixels, can be stored, transmitted, and processed using various techniques and algorithms.

In a discrete image, the visual information is quantized into discrete values. These values are typically integers that represent a range of colors or brightness levels. For example, in a grayscale image, each pixel may have a value between 0 and 255, where 0 represents black and 255 represents white. In a color image, each pixel is represented by a combination of three or more values, such as red, green, and blue (RGB) intensities. The overall structure of a discrete image is determined by the dimensions of the grid and the number of pixels in each dimension.

Applications of Discrete Images

Discrete images are the building blocks of various applications in engineering, science, and art. Here are a few examples of how discrete images are used in different domains:

1. Digital Photography: When you capture a photo using a digital camera, the scene is sampled and converted into a discrete image. This image can be stored, manipulated, and printed using digital techniques. The quality of the image depends on factors such as the resolution (number of pixels), color depth (number of possible color values per pixel), and dynamic range (difference between the darkest and brightest values).

2. Graphic Design: Many graphic design software, such as Adobe Photoshop, work with discrete images. Designers can create or edit images by manipulating individual pixels or groups of pixels. They can adjust colors, apply filters, add text, and merge multiple images together. By working with discrete representations, they have precise control over the visual elements.

3. Medical Imaging: Medical imaging technologies, like X-rays, CT scans, and MRIs, produce discrete images that help diagnose and monitor diseases and conditions. These images are essential for identifying abnormalities, planning surgeries, and tracking the progress of treatments. Advanced techniques, like image segmentation and 3D reconstruction, enable healthcare professionals to extract valuable information from the discrete images.

4. Autonomous Vehicles: In the context of self-driving cars and other autonomous vehicles, discrete images play a vital role in perception and navigation systems. Cameras mounted on the vehicles capture real-time scenes, which are then processed to identify objects, detect obstacles, and recognize traffic signs and signals. By analyzing discrete images, autonomous vehicles can make informed decisions and operate safely.

Frequently Asked Questions (FAQs)

Q1. How does a digital camera convert a continuous scene into a discrete image?
A digital camera’s image sensor is made up of millions of small light-sensitive elements called pixels. Each pixel converts the incoming light into an electrical signal that represents the intensity or color at that particular location. This analog data is then converted into discrete digital values through an analog-to-digital converter, resulting in a discrete image.

Q2. Can we convert a discrete image back into a continuous representation?
Although a discrete image is an approximation of a continuous scene, it is not possible to perfectly reconstruct the original continuous representation from the discrete data. Once the visual information is sampled, some details are lost, especially if the resolution is low. However, various interpolation techniques can be used to enhance the visual quality or estimate missing information based on the neighboring pixels.

Q3. Do all image formats represent discrete images?
Yes, all common image formats, such as JPEG, PNG, and GIF, represent discrete images. These formats use different compression algorithms to reduce the file size while maintaining acceptable visual quality. Regardless of the compression, the underlying structure remains discrete, and each pixel retains its individual value.

Q4. What are the advantages of working with discrete images?
Working with discrete images offers several advantages. First, discrete representations facilitate easy storage and transmission of visual data. Second, discrete images can be processed efficiently using various algorithms, such as filtering, edge detection, and feature extraction. Third, discrete images enable precise control over individual pixels and allow for sophisticated editing and manipulation.

Q5. How does the resolution of a discrete image affect its quality?
The resolution of a discrete image refers to the number of pixels in each dimension. Higher resolution images have more pixels, resulting in greater detail and clarity. The ability to discern fine details, such as sharp edges and small features, improves with higher resolution. However, higher resolution images require more storage space and processing power, and may not be necessary or practical for all applications.

Conclusion

In conclusion, a discrete image is a structured representation of visual information divided into pixels, each containing discrete values that represent specific attributes. Discrete images are used in various domains and applications, including digital photography, graphic design, medical imaging, and autonomous vehicles. Understanding the concept of discrete images is essential for working with digital imagery and unlocking the potential of modern technologies.

By providing a precise and well-defined representation of visual scenes, discrete images enable efficient storage, transmission, and processing of visual data. They form the backbone of numerous applications that impact our daily lives, from capturing memorable moments with digital cameras to ensuring the safe and reliable operation of autonomous vehicles.

Continuous image, also known as a continuous function or continuous mapping, is a fundamental concept in mathematics and has wide-ranging applications in various fields including physics, computer science, and engineering. In simple terms, a continuous image refers to a mapping between two sets where there are no abrupt changes or interruptions.

To understand the concept of a continuous image, it’s essential to grasp the notion of continuity. In mathematics, a function is said to be continuous if it preserves the nearness of points. In other words, as the input values get arbitrarily close to each other, the corresponding output values also get arbitrarily close. This implies that there are no significant jumps, holes, or breaks in the function.

Formally, let’s consider two sets A and B, and a function f that maps elements from A to B. The function f is said to be continuous if and only if for every point a in A, and for every positive number ε, there exists a positive number δ, such that for all points x in A that lie within a distance δ of a, the corresponding images f(x) in B lie within a distance ε of f(a).

Continuous images have several important properties and characteristics. Firstly, the composition of continuous functions is itself a continuous function. If we have two continuous functions f: A → B and g: B → C, then the composition g∘f: A → C is also continuous.

Secondly, continuous functions exhibit certain properties that allow for the simplification of calculations. For example, if a function is continuous on a closed interval, it must possess a maximum and minimum value on that interval. This property, known as the Extreme Value Theorem, is useful in optimization problems where finding the highest and lowest values of a function is of interest.

Additionally, continuous functions guarantee the preservation of certain properties between sets. For instance, if a set is open in A, then its image under a continuous function will also be open in B. Similarly, if a set is closed in A, then its image under a continuous function will also be closed in B.

Continuous images find significant applications in various fields. In physics, continuous functions are used to model and describe physical phenomena, such as motion or the behavior of waves. By assuming continuity, scientists and engineers can develop accurate models that capture real-world dynamics.

In computer science, continuous images play a crucial role in signal processing, computer vision, and image recognition. For instance, in image filtering or enhancement algorithms, continuity allows for the smooth transition of pixel values, resulting in visually appealing and realistic outcomes.

Moreover, continuous functions are extensively used in optimization, where finding the maximum or minimum value of a certain function is vital. By leveraging the properties of continuous images, mathematicians and scientists can solve complex optimization problems efficiently.

FAQs:

Q: What is the difference between continuous and discontinuous functions?
A: A continuous function does not have abrupt changes or interruptions, and its graph can be drawn without lifting a pencil. On the contrary, a discontinuous function exhibits abrupt changes, holes, or breaks in its graph.

Q: Can a function be continuous at one point and discontinuous at another?
A: Yes, it is possible. A function can exhibit different continuity behaviors at different points. For example, the function f(x) = 1/x is continuous everywhere except at x = 0.

Q: What are the necessary conditions for a function to be continuous?
A: A function is continuous if and only if it satisfies the three conditions: 1) The function is defined at that point, 2) The limit of the function as x approaches that point exists, and 3) The value of the function at that point is equal to the limit of the function at that point.

Q: Are all continuous functions smooth?
A: No, not all continuous functions are smooth. While continuous functions do not have abrupt changes, they can exhibit sharp bends, cusps, or other irregularities. Smooth functions, on the other hand, are infinitely differentiable with no sharp features.

Q: Are all continuous functions bounded?
A: No, not all continuous functions are bounded. A function can be continuous but have no upper or lower limits. For example, the function f(x) = x is continuous on the entire real line and is unbounded.

In conclusion, a continuous image represents a mapping between sets that preserves the nearness of points without abrupt changes or interruptions. This concept has numerous applications in mathematics, physics, computer science, and engineering. Understanding continuous functions and their properties enables us to model physical phenomena, solve optimization problems, and develop advanced image processing algorithms.

Continuous Image Math: Exploring Mathematical Concepts in the Digital Realm

In the digital era, the visual medium has become an integral part of our lives. From photographs to videos, images have the power to convey emotions, tell stories, and captivate our imagination. But behind these captivating visuals lies a world of mathematical concepts and algorithms that make it possible for us to capture, edit, and manipulate images. One such aspect of this fascinating domain is continuous image math, which bridges the gap between mathematics and the digital realm. In this article, we will delve into the realm of continuous image math, exploring its applications, techniques, and benefits.

What is Continuous Image Math?

Continuous image math refers to the application of mathematical concepts and algorithms to manipulate, process, and enhance images. Unlike discrete image math, which deals with digital images represented by a grid of pixels, continuous image math operates on images as a continuous function defined over a continuous domain. This allows for more precise and flexible transformations on images, leading to superior results in terms of quality and visual appeal.

Applications of Continuous Image Math

Continuous image math finds its applications across various fields, including computer graphics, image processing, computer vision, and even artistic endeavors. Some common applications include:

1. Image Restoration: Continuous image math enables the restoration of images that are corrupted or degraded due to noise, blur, or other artifacts. By modeling the degradation process mathematically, algorithms can reconstruct the original image, removing unwanted effects.

2. Image Compression: Continuous image math plays a crucial role in image compression techniques. By applying mathematical transformations such as discrete cosine transform (DCT) or wavelet transform, images can be efficiently represented using fewer bits, leading to reduced storage requirements and faster transmission over networks.

3. Image Morphing: Continuous image math provides the tools to warp and blend images seamlessly, enabling impressive morphing effects between two or more images. This technique has found significant applications in animation, special effects, and even plastic surgery simulations.

4. Image Segmentation: Continuous image math assists in segmenting objects within images by analyzing their boundaries and color gradients. This segmentation is essential in various applications, including object recognition, medical imaging, and video surveillance.

Techniques in Continuous Image Math

To achieve the desired transformations and enhancements in images, several mathematical techniques are employed in continuous image math. Some notable ones include:

1. Convolution: Convolution is a fundamental operation in continuous image math, where a function is combined with a kernel function to produce a modified version of the original function. In image processing, convolution is widely used for operations like blurring, sharpening, and edge detection.

2. Fourier Transform: The Fourier transform is a powerful mathematical tool that decomposes an image into a sum of sine and cosine waves of different frequencies. This transformation helps analyze the frequency content of an image and is widely used in image filtering and compression techniques.

3. Partial Differential Equations (PDEs): PDEs provide a rich set of mathematical formulations to describe and manipulate images. Techniques like diffusion, heat equation, and level set methods use PDEs to smooth images, remove noise, and segment objects within them.

4. Variational Methods: Variational methods offer a way to optimize image properties by formulating them as energy functionals. By minimizing these functionals, images can be enhanced or deformed based on specific criteria. Variational methods have been successfully applied in image denoising, colorization, and inpainting.

Benefits of Continuous Image Math

Continuous image math offers several advantages over discrete image math. Some key benefits include:

1. Improved Visual Quality: By operating on continuous functions, continuous image math results in smoother, more visually pleasing transformations and enhancements compared to their discrete counterparts.

2. Flexibility and Precision: Continuous image math allows for more precise control over image transformations due to the continuous nature of the operations. This enables fine-grained adjustments and customized modifications tailored to specific requirements.

3. Enhanced Realism: Continuous image math techniques, such as warping and morphing, enable the creation of realistic animations and effects, making them an invaluable tool in the entertainment industry.

4. Artistic Expression: Continuous image math has also found its place in the realm of digital art. Artists can use mathematical algorithms to create mesmerizing visual compositions, exploring the infinite possibilities of colors, shapes, and transformations.

Frequently Asked Questions (FAQs)

Q1. Is continuous image math only applicable to digital images?
A1. Continuous image math can be applied to both digital and analog images. However, in the context of digital image processing and computer graphics, the concepts and algorithms are tailored to operate on discrete digital images.

Q2. Do I need advanced mathematical knowledge to understand continuous image math?
A2. While a basic understanding of mathematical concepts is helpful, one can still appreciate and apply continuous image math techniques without delving too deeply into complex mathematics. Various software tools provide user-friendly interfaces to apply these techniques.

Q3. How can I get started with continuous image math?
A3. To get started, it is recommended to have a basic understanding of image processing and relevant mathematical concepts. There are numerous online resources, tutorials, and textbooks available that cover the fundamentals of continuous image math.

Q4. Are there any limitations to continuous image math?
A4. Continuous image math has its limitations, particularly in terms of computational complexity. Some advanced techniques may require significant computational resources to achieve real-time processing. However, continuous image math continues to advance, addressing such limitations and opening new avenues for exploration.

In conclusion, continuous image math serves as a bridge between the worlds of mathematics and the digital realm. It offers a wide range of applications and techniques that enhance our ability to capture, manipulate, and appreciate the visual medium. By understanding and exploring this fascinating field, we can unlock new possibilities in the realms of art, science, technology, and beyond.

Found 25 images related to what is discrete and continuous values of image theme