Aliased Coefficients In The Model: Unveiling The Hidden Structures

Explaining Aliased Coefficients in a Model

In statistical modeling, aliased coefficients refer to the situation where two or more regression coefficients are linearly dependent, leading to a lack of identifiability in the model. This means that it is impossible to uniquely estimate the values of these coefficients. Aliased coefficients can arise due to various reasons such as multicollinearity or overparameterization of the model.

Aliased coefficients can cause issues in terms of model interpretation and parameter estimation. It becomes difficult to determine the individual effects of the predictors on the response variable, as the coefficients are not uniquely identifiable. As a result, the interpretation of the model becomes challenging, and it becomes unclear which predictors have a significant impact on the response variable.

Identifying Aliased Coefficients

There are several techniques available to identify aliased coefficients in a model. One commonly used method is the Variance Inflation Factor (VIF). VIF measures the severity of multicollinearity in the model by calculating the ratio of the variance of a coefficient to the variance of that coefficient when all predictors are uncorrelated. Higher VIF values indicate a higher degree of multicollinearity and potential aliasing issues.

VIF in R is a function that can be used to compute the VIF values for each coefficient in a linear regression model. However, if you encounter the error “Could not find function vif” in R, it means that the VIF function is not available in the current environment. To resolve this, you can load the necessary package that contains the VIF function. The “car” package is commonly used for computing VIF in R. You can install and load the “car” package using the following commands in R:

install.packages(“car”)
library(car)

Once the package is loaded, the vif() function can be used to compute the VIF values for each coefficient in the model, allowing you to identify potential aliased coefficients.

Dealing with Aliased Coefficients: Regularization Methods

When aliased coefficients are identified in a model, it is necessary to handle them appropriately to ensure reliable parameter estimation and robust model interpretation. One common approach to dealing with aliased coefficients is through regularization methods.

Regularization is a technique used to introduce a penalty term in the estimation process, which helps in shrinking the coefficient estimates towards zero. This regularization helps in mitigating the impact of multicollinearity and reducing the degree of aliasing. Two popular regularization techniques are Ridge Regression and Lasso Regression.

Ridge Regression adds a penalty term to the least squares estimation, which prevents the coefficients from becoming too large. By doing so, it reduces the impact of multicollinearity and helps to deal with aliased coefficients effectively. Lasso Regression, on the other hand, introduces a penalty term that encourages some of the coefficients to be exactly zero, resulting in a sparse model with fewer aliased coefficients.

Strategies for Resolving Aliased Coefficients

Apart from regularization techniques, there are other strategies that can be employed to resolve aliased coefficients in a model. One approach is to drop or remove the predictors that are causing the multicollinearity issue. By eliminating highly correlated predictors, the multicollinearity is reduced, and the chances of aliased coefficients occurring are minimized.

Another strategy is to collect more data, which can help in reducing the impact of multicollinearity and resolving the issue of aliased coefficients. With a larger sample size, the relationships between the predictors become more discernible, and the extent of multicollinearity can be better understood.

Importance of Addressing Aliased Coefficients in Statistical Modeling

Addressing aliased coefficients is crucial in statistical modeling as it impacts both the parameter estimation and the interpretation of the model. Without resolving the issue of aliased coefficients, it is difficult to identify the true effects of the predictors and make accurate predictions.

By identifying and handling aliased coefficients appropriately, we can ensure a more reliable and interpretable model. Regularization techniques and other strategies help in mitigating the impact of multicollinearity and resolving the issue of aliased coefficients.

FAQs:

Q: What does it mean when coefficients are aliased in a model?
A: When coefficients are aliased in a model, it means that they are linearly dependent, making it impossible to uniquely estimate their values.

Q: How can I identify aliased coefficients in my model?
A: One commonly used method to identify aliased coefficients is the Variance Inflation Factor (VIF). Higher VIF values indicate a higher degree of multicollinearity and potential aliasing issues.

Q: What should I do if I encounter the error “Could not find function vif” in R?
A: If you encounter this error, it means that the VIF function is not available in the current environment. You can resolve this by loading the necessary package that contains the VIF function, such as the “car” package.

Q: Are there other ways to deal with aliased coefficients besides regularization methods?
A: Yes, there are other strategies to resolve aliased coefficients, such as dropping or removing highly correlated predictors from the model or collecting more data to reduce the impact of multicollinearity.

Q: Why is it important to address aliased coefficients in statistical modeling?
A: Addressing aliased coefficients is important as it impacts both the parameter estimation and the interpretation of the model. Without resolving aliased coefficients, it becomes difficult to identify the true effects of predictors and make accurate predictions.

What are Aliased Coefficients in the Model?

In statistical modeling, particularly in regression analysis, the term “aliased coefficients” refers to a situation where two or more coefficients in the model are not uniquely identifiable. Aliasing occurs when there is a perfect or near-perfect linear relationship among the variables included in the model, leading to redundant information and resulting in coefficients that cannot be estimated separately. Understanding the concept of aliased coefficients is important for ensuring accurate interpretations of regression model outputs and making meaningful inferences.

Aliasing arises due to the intrinsic relationships between variables, either based on the nature of the data or the design of the study. When two or more variables have a strong linear association, their individual effects on the outcome variable cannot be precisely estimated, as the model fails to distinguish their independent contributions. Instead, the model estimates a weighted combination of the effects, known as the aliased coefficients.

The concept is best understood through an example. Imagine a simple linear regression model that aims to predict a person’s weight based on their height and age. If height and age are highly correlated in the dataset, it becomes difficult to separate their individual impacts on weight. The model may assign a positive coefficient to height, indicating that taller individuals tend to weigh more. However, the estimated coefficient for age may be negative, suggesting that older individuals weigh less, even if it contradicts reality. This inconsistent interpretation occurs because height and age both contribute to variations in weight, but their individual effects cannot be accurately determined.

To identify aliased coefficients, statisticians use a technique called linear dependency testing. This involves examining the matrix of independent variables in the regression model to identify redundant columns, meaning that one variable can be expressed as a linear combination of others. Various methods, such as calculating the determinant of the matrix or using matrix rank, can be employed to assess the presence of linear dependencies. Once aliased coefficients are identified, statisticians may need to take corrective actions, such as removing redundant variables or transforming variables to break the linear relationship, in order to obtain valid estimates.

FAQs:

Q: Why are aliased coefficients problematic?
A: Aliased coefficients pose challenges in model interpretation and inference. When two or more coefficients are aliased, it becomes impossible to disentangle the independent effects of those variables. This undermines the scientific understanding of the studied phenomenon and hampers the ability to make accurate predictions based on the model.

Q: How can one avoid or manage aliased coefficients?
A: Avoiding aliased coefficients typically involves careful study design and data collection. Ensuring a diverse and independent set of variables reduces the likelihood of aliased coefficients. However, if such dependencies are discovered in the model, various remedies can be applied. These include removing redundant variables, combining correlated variables into composite measurements, employing more advanced statistical techniques, or collecting additional data to overcome the limitations.

Q: Can aliased coefficients lead to biased results?
A: Yes, aliased coefficients can lead to biased estimates of the regression coefficients. Bias occurs when the model incorrectly assigns the effects of correlated variables to other coefficients. As a result, the estimated coefficients may be far from their true values, leading to incorrect interpretations and potentially flawed conclusions.

Q: Are aliased coefficients always problematic?
A: Aliasing only becomes problematic if it hinders accurate interpretation or prediction. In some cases, the goal may not be to estimate individual effects but rather to understand the overall effect of a group of variables. In such situations, aliased coefficients may not pose a significant issue. However, it is essential to be cautious and aware of the limitations imposed by aliased coefficients when making inferences.

Q: Can aliasing be completely avoided in regression modeling?
A: Completely avoiding aliasing is challenging because it depends on the intricate relationships between variables. However, statisticians and researchers can take preventive measures by carefully selecting variables and considering underlying correlations during the model design phase. Additionally, employing advanced modeling techniques, such as ridge regression or principal component analysis, may help mitigate the effects of potential aliases.

In summary, aliased coefficients in a regression model arise when two or more variables have a strong linear relationship and their independent impacts cannot be accurately estimated. It is important to identify and manage aliased coefficients to ensure valid interpretations and reliable predictions. By understanding the implications of aliased coefficients and employing appropriate corrective measures, statisticians can enhance the accuracy and robustness of their regression models.

What are the Coefficients of a Model?

In the field of statistics and machine learning, a model is a mathematical representation of a system, process, or phenomenon. Models are used to make predictions, understand relationships between variables, and gain insights from data. One crucial component in these models is the coefficients.

Coefficients, also commonly referred to as parameters or weights, are numerical values assigned to the variables in a model. They play a fundamental role in determining the behavior and performance of the model. In this article, we will explore the concept of coefficients in depth and understand their significance in different types of models.

Understanding Coefficients:

To grasp the importance of coefficients, let’s consider the simplest form of a model known as the linear regression model. In this model, the relationship between a dependent variable (Y) and a set of independent variables (X1, X2, X3,…,Xn) is represented as a linear equation:

Y = β0 + β1X1 + β2X2 + β3X3 + … + βnXn + ε

Here, β0, β1, β2,…,βn are the coefficients, X1, X2,…,Xn are the independent variables, and ε is the error term. The coefficients quantify the impact of each independent variable on the dependent variable.

Coefficients provide information about the magnitude and direction of the relationship between variables. A positive coefficient indicates a direct relationship where an increase in the independent variable leads to an increase in the dependent variable, while a negative coefficient implies an inverse relationship. The absolute value of the coefficient represents the strength of the relationship.

Estimating Coefficients:

To build a model, we must estimate the coefficients that best fit the data. This process involves finding the values that minimize the difference between the actual data points and the values predicted by the model. One common approach to estimating coefficients is called Ordinary Least Squares (OLS).

OLS determines the coefficients by minimizing the sum of the squared differences between the predicted values and the actual values. This method ensures that the model captures the underlying patterns in the data.

In more complex models, such as logistic regression or neural networks, estimating coefficients becomes more intricate. Various optimization algorithms, such as gradient descent, are utilized to iteratively adjust the coefficients until they converge to the optimal values.

Interpreting Coefficients:

Once the coefficients have been estimated, it is essential to interpret their values correctly. The interpretation depends on the type of model being used.

In linear regression models, the coefficients indicate the change in the dependent variable for a unit change in the corresponding independent variable, holding all other variables constant. For example, if the coefficient of a variable is 0.5, it means that a 1-unit increase in that variable is associated with a 0.5-unit increase in the dependent variable.

In logistic regression models, the coefficients represent the logarithm of the odds ratio. They indicate the impact of the independent variables on the probability of an event occurring. Similar to linear regression models, a positive coefficient implies an increase in the odds of the event, while a negative coefficient implies a decrease.

Coefficients in Machine Learning Models:

The use of coefficients extends beyond traditional statistical models. In machine learning, numerous algorithms employ coefficients to optimize the model’s performance. Some examples include decision trees, random forests, support vector machines, and deep learning models.

In decision tree algorithms, coefficients, referred to as feature importance, quantify the significance of each variable in splitting the data. The importance values help identify the most influential features in the decision-making process.

Random forests combine multiple decision trees and calculate feature importance by aggregating the contributions of individual trees. The coefficients rank the variables based on their predictive power, allowing for feature selection and interpretation.

Support vector machines and deep learning models also rely on coefficients to assign weights to the variables. These weights determine the contribution of each variable to the overall decision boundary of the model.

FAQs:

Q: Can coefficients have negative values?
A: Yes, coefficients can indeed have negative values. Negative coefficients indicate an inverse relationship between the independent and dependent variables.

Q: Are coefficients the same as correlation coefficients?
A: No, they are not the same. Coefficients in a model, such as linear regression or logistic regression, represent the impact of independent variables on the dependent variable. Correlation coefficients, on the other hand, measure the strength and direction of the linear relationship between two variables.

Q: Do coefficients remain the same in every instance of a model?
A: No, coefficients can change for each instance of a model, especially when the data or the model is updated or modified. Coefficients are estimated based on the available data and may differ if new data is introduced or the model structure is altered.

Q: How can coefficients be used for feature selection?
A: Coefficients, such as feature importance in decision trees or random forests, can be used for feature selection. Variables with higher coefficients are considered more important, and those with lower coefficients can be eliminated to simplify the model.

Q: Are coefficients unique for each model?
A: Yes, coefficients are unique to each model. Different models may produce different coefficient values even if they use the same set of variables.

Could not find function vif: A Guide to Addressing the Issue

Introduction:
When using statistical analysis tools like R or Python for regression modeling, you may come across an error message stating “Could not find function vif.” This error occurs when the code attempts to utilize the vif (variance inflation factor) function, commonly used to check for multicollinearity in regression models. In this article, we will explore the possible reasons for this error message and provide actionable solutions to resolve this issue.

Understanding Multicollinearity and the VIF:
Multicollinearity refers to a situation when two or more independent variables in a regression model are highly correlated, leading to instability and unreliable estimates. It is crucial to identify and address multicollinearity, as it can affect the interpretation and inference of regression model results.

The variance inflation factor (VIF) is a statistical measure that quantifies the extent of multicollinearity between independent variables. A high VIF value indicates a strong correlation between two or more variables, suggesting the presence of multicollinearity. By identifying and addressing multicollinearity, we can improve the accuracy and reliability of our regression models.

Possible Causes of the “Could not find function vif” Error:
1. Missing Packages: The vif function is usually not available by default in statistical analysis tools such as R or Python. It belongs to specific packages, and if those packages are not installed, the error message may occur. The ‘car’ package in R and the ‘statsmodels’ package in Python are commonly used to perform VIF calculations.

2. Typo or Capitalization: It is essential to ensure correct spelling and punctuation while coding. A simple typo or capitalization error can result in an error message such as “Could not find function vif.” Double-check the function name and its syntax to eliminate this possibility.

3. Package Not Loaded: Even if you have installed the required package, you need to load it explicitly in your R or Python session. In R, you can use the ‘library()’ or ‘require()’ functions, while in Python, you can use the ‘import’ statement to load the package. Failing to load the package will cause the function vif to be unrecognized.

Solutions to Resolve the “Could not find function vif” Error:
1. Install the Required Package: If you have not installed the necessary package (e.g., ‘car’ in R or ‘statsmodels’ in Python), you can install it using the package installation functions specific to your statistical analysis tool. In R, you can use the ‘install.packages()’ function, while in Python, you can use the ‘pip install’ command. Ensure that you have the correct package name and version for your tool.

2. Load the Package: After installing the required package, load it into your R or Python session using the appropriate commands. In R, you can use ‘library(car)’ or ‘require(car)’. In Python, you can use ‘import statsmodels.api as sm’.

3. Check for Typos: Carefully review your code to ensure that there are no typos or capitalization errors when invoking the vif function. A small mistake can lead to the “Could not find function vif” error. Compare your code with documentation or examples to verify the correct spelling.

Frequently Asked Questions (FAQs):

Q1: Can I use a different function or method to check for multicollinearity if I cannot find the vif function?
A1: Yes, there are alternative methods to assess multicollinearity. In R, you can use the ‘cor()’ function to calculate variable correlations or perform a principal component analysis (PCA). In Python, you can use the ‘corr()’ function from the ‘pandas’ library or calculate the condition number using ‘numpy’ packages. These methods can provide insights into multicollinearity similar to the VIF.

Q2: I have installed the required package and ensured correct syntax, but I still encounter the error. What can I do?
A2: It is possible that the package version is not compatible with your current environment or other packages. Try updating the package to the latest version using the appropriate package management functions, such as ‘update.packages()’ in R or ‘pip install –upgrade’ in Python. If the error persists, seek help from online forums or consult the package documentation.

Q3: Are there any alternative packages or libraries available to compute the VIF in R or Python?
A3: Yes, other packages and libraries also provide functions to calculate the VIF. In R, you can use ‘usdm’ or ‘leaps’ packages. In Python, you can use the ‘ols’ function from the ‘linearmodels’ library. These packages provide similar functionality and can help you overcome the “Could not find function vif” error.

Conclusion:
The “Could not find function vif” error often occurs when attempting to assess multicollinearity in regression analysis. This error can be resolved by checking for missing packages, loading the correct package, and ensuring the correct syntax. If you encounter persistent issues, consider alternative packages or methods for assessing multicollinearity. Remember, addressing multicollinearity is vital for accurate regression modeling and robust statistical analysis.

VIF in R: A Comprehensive Analysis for Multicollinearity Detection

Introduction
In statistical modeling, multicollinearity refers to the high correlation between independent variables in a regression model. Multicollinearity can cause several issues in regression analysis, such as unstable coefficient estimates, reduced interpretability, and decreased predictive power. In order to detect and mitigate multicollinearity, one useful tool is the Variance Inflation Factor (VIF). In this article, we will explore VIF in R, its calculation, interpretation, and how to handle multicollinearity using this statistical technique.

Understanding VIF
The Variance Inflation Factor (VIF) quantifies the degree of multicollinearity between explanatory variables in a regression model. It measures how much the variance of the estimated regression coefficient is increased due to multicollinearity. VIF values greater than 1 suggest multicollinearity, with values over 5 or 10 often considered problematic.

Calculating VIF in R
To calculate VIF in R, we can utilize the “vif()” function available in the “car” package. Before calculating VIF, it is necessary to fit a regression model using the data of interest. Then, the “vif()” function can be applied to the fitted model to obtain the VIF values for each independent variable. Consider the example below:

“`R
library(car)
model <- lm(dependent_variable ~ independent_variable1 + independent_variable2 + independent_variable3, data = dataset) vif_values <- vif(model) ``` In this code snippet, a multiple linear regression model is created using the "lm()" function, where "dependent_variable" is the outcome variable, and "independent_variable1," "independent_variable2," and "independent_variable3" are the predictor variables. The dataset used should contain these variables. The "vif()" function then calculates the VIF values based on the fitted model. Interpreting VIF Values Interpreting VIF values is crucial for identifying multicollinearity. Generally, VIF values over 1 indicate some degree of multicollinearity. A VIF of exactly 1 suggests no correlation, while values greater than 1 imply the presence of multicollinearity. Typically, a common threshold is a VIF of 5 or 10, where values exceeding this indicate significant multicollinearity. Handling Multicollinearity with VIF Once multicollinearity is identified using VIF, it is essential to take corrective measures. Several strategies can be employed to mitigate the impact of multicollinearity: 1. Variable Selection: Identifying and removing variables that contribute the most to multicollinearity can help improve the model. Further analysis, such as examining correlations and domain knowledge, can guide this process. 2. Combination of Variables: Sometimes, creating new variables by combining highly correlated variables can reduce multicollinearity. This process is known as variable transformation. Techniques like principal component analysis (PCA) or factor analysis can be employed to create linear combinations of variables. 3. Ridge Regression: Ridge regression is a technique that applies a penalty to the regression coefficients, reducing the impact of multicollinearity. The Ridge regression model introduces a tuning parameter that can be adjusted to control the amount of shrinkage in the coefficients. This method can assist in stabilizing the estimates and reducing the impacts of multicollinearity. Frequently Asked Questions (FAQs): Q: Can VIF values be negative? A: No, VIF values cannot be negative. Negative values indicate an inappropriate model specification or a statistical error. Q: Is VIF reliable for detecting multicollinearity? A: VIF is a widely used technique to detect multicollinearity in linear regression models. However, it is important to note that it only identifies pairwise multicollinearity, meaning it assesses the relationship between two variables at a time. It may not capture more complex forms of multicollinearity, such as interactions. Q: What is the significance of the VIF threshold? A: The threshold is used as a guideline, indicating a level beyond which multicollinearity is considered problematic. The specific threshold value to consider as problematic may vary depending on the context and specific analysis. It is crucial to exercise judgment and consider other factors alongside the VIF values. Q: Can VIF values differ between datasets? A: Yes, VIF values can differ between datasets, as the presence and intensity of multicollinearity can vary depending on the specific dataset and variables under consideration. Therefore, it is essential to calculate VIF values for each individual dataset. Conclusion Variance Inflation Factor (VIF) is a powerful tool for detecting multicollinearity in regression models. By calculating VIF for each independent variable, researchers and analysts can identify and manage multicollinearity effectively. Insights gained from VIF can guide variable selection, variable transformation, or the application of techniques like ridge regression. In conclusion, the understanding and careful consideration of VIF values can significantly improve the quality and reliability of statistical analyses.

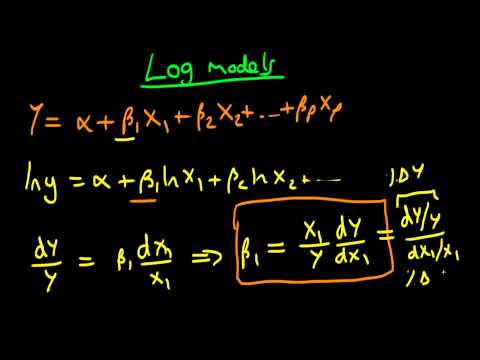
Found 6 images related to there are aliased coefficients in the model theme