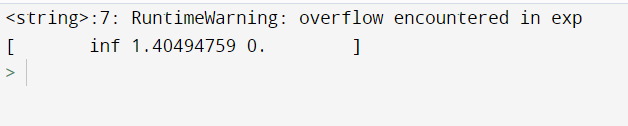
Runtimewarning: Overflow Encountered In Exp
Overflow encountered in exp sigmoid is a specific type of overflow warning that occurs when using the sigmoid function in numpy, which relies on the exponential function. The sigmoid function is commonly used in machine learning and deep learning algorithms for modeling binary classification problems, where it maps any input value to a value between 0 and 1. When the input to the sigmoid function is very large, the exponential calculation can result in overflow, causing the warning message.
Runtimewarning: Overflow encountered in int_scalars is another variation of the overflow warning. This warning occurs when performing calculations involving scalar integers and encountering values that are too large to be represented accurately within the data type’s range. The warning is raised to alert the programmer about potential loss of precision or incorrect results due to this overflow.
RuntimeWarning: Divide by zero encountered in log is a warning that appears when attempting to take the logarithm of zero or a negative number. Since the logarithm function is not defined for these values, the warning is raised to notify the programmer about the invalid operation.
RuntimeWarning: Invalid value encountered in subtract is a warning that occurs when performing a subtraction operation that results in an invalid value, such as subtracting infinity from infinity or subtracting NaN (Not a Number) from a valid number. This warning indicates that the result of the subtraction is undefined or does not conform to mathematical rules.
Np exp is a shorthand for the exponential function provided by the numpy library. The numpy.exp() function calculates the exponential value of each element in the input array. It is a commonly used function in scientific computing and data analysis applications.
Invalid value encountered in true_divide occurs when performing a division operation where the denominator is zero or results in an invalid value, such as infinity divided by infinity. The true_divide function in numpy calculates the quotient of two arrays element-wise and raises this warning when encountering such invalid values.
Invalid value encountered in double_scalars is a warning that occurs when performing a mathematical operation involving floating-point values and encountering an invalid result. This warning can be raised when dividing a floating-point number by zero or when performing other arithmetic operations that result in invalid values.
To handle or prevent these runtime warnings, several strategies can be employed:
1. Scaling or Normalizing Input: When encountering overflow warnings, it can be helpful to rescale or normalize the input values to prevent extremely large inputs. This can be achieved by applying appropriate scaling techniques to the data before performing calculations involving exponential or other functions.
2. Handling Division by Zero: To avoid the “divide by zero” warnings, it is crucial to check for zero denominators or invalid values before performing division operations. This can be done using conditional statements or by applying numpy’s masking or filtering capabilities.
3. Using alternative functions or techniques: In some cases, it may be possible to replace the exponential function with other approximations or strategies that do not result in overflow. For example, the use of logarithmic transformations or alternative sigmoid functions could be considered as potential replacements.
4. Suppression of Warnings: If the warnings are not critical and do not affect the desired outcomes of the calculations, they can be suppressed using the warnings module in Python. However, it is generally recommended to address the root cause of the warnings rather than suppressing them blindly.
In conclusion, the RuntimeWarning: Overflow encountered in exp is a common warning message in Python that arises when exponential calculations encounter extremely large input values. This warning, along with other related warnings mentioned in this article, serves as an indicator of potential precision loss, invalid results, or undefined operations. By employing appropriate techniques such as scaling, handling division by zero, or using alternative functions, programmers can mitigate the impact of these warnings and ensure accurate and reliable computations with numpy.
FAQs:
Q: What does the warning “Overflow encountered in exp” mean?
A: This warning occurs when performing exponential calculations with extremely large input values, resulting in an overflow error.
Q: How can I handle the “divide by zero” warning?
A: It is important to check for zero denominators or invalid values before performing division operations. Conditional statements or numpy’s masking/filtering capabilities can help in handling these cases.
Q: Can I suppress these warnings?
A: Yes, you can suppress the warnings using the warnings module in Python. However, it is generally recommended to address the root cause of the warnings rather than suppressing them blindly.
Q: Are there alternative functions or techniques to prevent overflow?
A: Yes, in some cases, you can replace the exponential function with other approximations or strategies that do not result in overflow. Logarithmic transformations or alternative sigmoid functions could be considered as potential replacements.
Q: When do I encounter “Invalid value encountered in subtract” warning?
A: This warning occurs when performing a subtraction operation that results in an undefined or invalid value, such as subtracting infinity from infinity or subtracting NaN from a valid number.
Python : Python Runtimewarning: Overflow Encountered In Long Scalars
Keywords searched by users: runtimewarning: overflow encountered in exp Overflow encountered in exp sigmoid, Runtimewarning overflow encountered in int_scalars, RuntimeWarning: divide by zero encountered in log, RuntimeWarning: invalid value encountered in subtract, Np exp, Invalid value encountered in true_divide, Invalid value encountered in double_scalars, Np exp() trong Python
Categories: Top 88 Runtimewarning: Overflow Encountered In Exp
See more here: nhanvietluanvan.com
Overflow Encountered In Exp Sigmoid
Overflow occurs when a value exceeds the maximum range representable by a numerical data type. In the context of exponential sigmoid, overflow typically arises due to the exponential function’s rapid increase for large positive inputs. This can cause numerical instability and disrupt the overall accuracy of computations. The sigmoid function, often used in machine learning and neural networks, is especially susceptible to this issue, as it relies heavily on exponential operations.
To better understand overflow in exponential sigmoid, let’s explore the mathematical formulation of the sigmoid function:
S(x) = 1 / (1 + e^(-x))
In this equation, e represents Euler’s number, an irrational constant approximately equal to 2.71828. As x approaches positive or negative infinity, the term e^(-x) rapidly diminishes to zero or becomes extremely large, respectively. Consequently, the denominator of the sigmoid function approaches zero or becomes extremely small, leading to computational errors.
Overflow not only affects the accuracy of the sigmoid function itself but also has a cascading effect on subsequent computations. For instance, in neural networks, the sigmoid function is frequently used as an activation function in hidden layers or as a final non-linear transformation for binary classification. If overflow occurs in the sigmoid function, the subsequent layers and output calculations will be impacted, potentially causing the entire network to yield erroneous results.
Fortunately, several strategies can be employed to mitigate or prevent overflow in exponential sigmoid:
1. Value Clipping: One straightforward approach is to clip the input value of the exponential function to a predefined range. By limiting the magnitude of the input x, we ensure that the exponential operation does not produce extremely large values, reducing the likelihood of overflow. However, this method may sacrifice precision and potentially distort the function’s intended behavior.
2. Numerical Approximation and Reformulation: Another approach involves utilizing alternative mathematical formulations or approximations of the sigmoid function. For instance, the hyperbolic tangent function (tanh) is often employed, as it exhibits similar characteristics to sigmoid but avoids many of the overflow-related issues. Additionally, the re-parameterization of the sigmoid function, such as using log-sum-exp or softplus functions, can provide additional stability and accuracy.
3. Logarithmic Transformations: Taking a logarithmic transformation of the sigmoid function can help enhance numerical stability and prevent overflow. By using properties of logarithms, we can transform the exponential sigmoid into an alternative form that reduces the likelihood of encountering overflow. However, this approach requires additional computations and may introduce some approximation errors.
4. Data Normalization: Scaling the input data within a reasonable range can alleviate overflow concerns. By shifting and rescaling the values, we ensure that the exponential operations encounter manageable ranges, reducing the risk of overflow. Nevertheless, this method requires careful selection of normalization parameters to preserve the integrity of the data.
5. Enhanced Numerical Precision: In some cases, employing higher-precision data types, such as double-precision floating-point numbers, can help overcome overflow issues. These data types allow for more significant ranges and greater precision, reducing the probability of overflow. However, this approach may come at the cost of increased memory usage and computational complexity.
FAQs:
Q: What are the potential consequences of overflow in exponential sigmoid?
A: Overflow can lead to inaccurate or incorrect calculations in the sigmoid function, affecting subsequent computations and potentially compromising the integrity of the entire system.
Q: Do these overflow issues only occur in sigmoid functions?
A: No, overflow issues can arise in various mathematical functions that rely on exponential operations. However, sigmoid functions are particularly susceptible due to their heavy reliance on exponential calculations.
Q: Can overflow be completely eliminated?
A: While it is challenging to eliminate overflow entirely, employing appropriate strategies, such as value clipping, numerical approximation, or data normalization, can significantly reduce the likelihood and impact of overflow.
Q: Are there any computational costs associated with tackling overflow?
A: Some mitigation strategies, such as higher-precision data types or more complex approximations, may introduce additional computational costs. However, these costs are often outweighed by the benefits of enhanced numerical stability and accuracy.
Q: Are there any potential drawbacks to using alternative sigmoid formulations?
A: Alternative formulations of the sigmoid function may exhibit slightly different characteristics and behaviors compared to the standard sigmoid function. Hence, careful consideration and testing must be conducted to ensure that the desired properties are preserved.
In conclusion, overflow encountered in exponential sigmoid poses challenges to accurate computational results, particularly in functions reliant on exponential operations like the sigmoid function. Employing strategies such as value clipping, numerical approximations, logarithmic transformations, data normalization, or enhanced numerical precision can help mitigate these issues effectively. By addressing overflow concerns, we can ensure the reliability and accuracy of the computations, especially in areas like machine learning where the sigmoid function plays a vital role.
Runtimewarning Overflow Encountered In Int_Scalars
When working with numerical computations and calculations, it is not uncommon to come across various warnings and error messages. One such warning you may encounter is the RuntimeWarning: overflow encountered in int_scalars. This warning typically indicates that an arithmetic operation has resulted in a value that is too large to be represented by the data type used, specifically with integer scalars.
In this article, we will delve deeper into the RuntimeWarning: overflow encountered in int_scalars warning, exploring its causes, implications, and possible solutions. So, let’s get started.
Causes of RuntimeWarning: overflow encountered in int_scalars
The RuntimeWarning: overflow encountered in int_scalars warning is often triggered when performing arithmetic operations that exceed the maximum value that an integer scalar can hold. Integer scalars have finite ranges, and if an operation exceeds this limit, an overflow occurs.
For example, consider the following snippet of code:
“`python
x = 2**31
y = x * 2
“`
In this scenario, the value of x is the maximum positive value that a 32-bit signed integer can store (2147483648). However, when we multiply x by 2, we end up with a value (4294967296) that surpasses the maximum value that the integer scalar can hold. Consequently, Python raises the RuntimeWarning: overflow encountered in int_scalars warning.
Implications and Risks
While the RuntimeWarning: overflow encountered in int_scalars warning may not necessarily result in immediate errors or crashes, it is worth investigating and addressing. Ignoring this warning can lead to incorrect calculations, data corruption, or unintended side effects in your program.
Additionally, the warning might indicate that you are working with values that are too large to be handled by integer scalars efficiently. In such cases, it is advisable to consider using alternative data types, such as floating-point numbers or long integers, depending on your specific requirements.
Solutions and Strategies
When faced with the RuntimeWarning: overflow encountered in int_scalars warning, there are a few strategies and solutions you can consider:
1. Use a Larger Data Type: One of the simplest solutions is to switch to a data type that can accommodate larger values, such as long integers. In Python, long integers provide arbitrary precision and can handle extremely large numbers with ease. Instead of using integers, you can define your variables as long integers by appending ‘L’ to the end, e.g., x = 2**31L.
2. Implement Error Handling: You can utilize try-except blocks to catch the RuntimeWarning and handle it gracefully. By encapsulating the problematic code inside a try block and catching the exception, you can display a custom error message or perform alternative computations whenever an overflow occurs. For instance:
“`python
try:
# Your code with potential overflow
except RuntimeWarning:
# Handle the overflow gracefully
“`
3. Optimize Your Algorithm or Logic: In some cases, encountering the RuntimeWarning: overflow encountered in int_scalars warning might indicate that your algorithm or logic needs optimization. Investigate whether there is a more efficient way to perform the calculations or if certain steps can be simplified to avoid exceeding the limits of integer scalars.
4. Utilize Numpy and NumPy Arrays: If you frequently deal with large numerical computations, utilizing the NumPy library can be beneficial. NumPy provides support for arrays with larger capacities, allowing for efficient manipulation of numerical data without running into overflow warnings. By using NumPy arrays, you can perform calculations on large datasets without encountering int_scalar overflow.
5. Consider Using Arbitrary-Precision Libraries: For highly specialized scenarios that demand extreme precision, libraries like SymPy or the GNU Multiple Precision Arithmetic Library (GMP) can be invaluable. These libraries offer arbitrary-precision arithmetic, enabling computations with numbers of practically unlimited size.
Frequently Asked Questions (FAQs)
Q: Can ignoring the RuntimeWarning: overflow encountered in int_scalars warning cause serious issues?
A: Ignoring this warning can lead to incorrect calculations, data corruption, or unintended side effects in your program. It is advisable to investigate and address the warning appropriately.
Q: Are there any performance implications when using larger data types?
A: Using larger data types, such as long integers or floating-point numbers, can have a minor impact on performance compared to standard integer scalars. However, the benefits of accurate computations and avoiding overflow issues often outweigh the negligible performance difference.
Q: How can I determine the maximum value a specific data type can hold?
A: In Python, you can use the sys module’s maxsize attribute to obtain the maximum value that can be stored by different data types. For instance, sys.maxsize will provide the maximum value for signed integer scalars.
Q: Are there any alternatives to manually handling the overflow warnings?
A: Yes, as mentioned earlier, you can use NumPy arrays or libraries like SymPy, GMP, or other arbitrary-precision libraries to handle larger computations and prevent overflow warnings from occurring in the first place.
In conclusion, the RuntimeWarning: overflow encountered in int_scalars warning indicates that an arithmetic operation has resulted in a value too large to be represented by the integer scalar data type used. To address this issue, consider using larger data types, optimize your algorithm, implement error handling, or leverage specialized libraries like NumPy or SymPy. Properly handling this warning will ensure accurate calculations and prevent potential issues.
Runtimewarning: Divide By Zero Encountered In Log
When this warning occurs, it indicates that a logarithmic function encountered a division by zero. Logarithmic functions are mathematical operations that involve calculating the inverse of exponentiation. In mathematical terms, the logarithm of a number x to a given base b is denoted as log(base b)(x) and can be represented as y = log(base b)(x). The logarithm measures the exponent to which the base must be raised to obtain the given value.
Now, let’s understand the reasons behind encountering this warning in Python code. When we try to calculate the logarithm of a number that is less than or equal to zero (including zero itself), it results in an undefined value. Logarithms can only be calculated for positive real numbers. As a result, Python raises a RuntimeWarning to alert the programmer about this mathematical inconsistency.
To better understand this, let’s consider an example:
“`python
import math
x = 0
result = math.log(x)
print(result)
“`
Executing this code will trigger the RuntimeWarning: divide by zero encountered in log. The reason is simply that we are attempting to compute the logarithm of 0, which is an invalid operation in mathematics.
To handle this warning and prevent the code from crashing, there are a few different strategies we can implement. One possible solution is to add conditional statements to check if the denominator is zero before performing any mathematical operations. By checking if the value is greater than zero, we can ensure that we are operating on valid inputs. Here’s an example:
“`python
import math
x = 0
if x > 0:
result = math.log(x)
print(result)
else:
print(“Invalid input: x must be greater than zero.”)
“`
In this modified code, we first verify if the input is greater than zero before calculating the logarithm. If x is less than or equal to zero, we print an error message instead of attempting the calculation. By utilizing this conditional approach, we can prevent the RuntimeWarning from being raised.
Another approach is to use exception handling with the try and except blocks. We can catch the specific exception, ZeroDivisionError, that occurs when a division by zero is encountered. We can then handle this exception gracefully, displaying suitable error messages or executing alternative code. Here’s an example:
“`python
import math
x = 0
try:
result = math.log(x)
print(result)
except ZeroDivisionError:
print(“Invalid input: x must be greater than zero.”)
“`
This code utilizes the try-except block to handle the ZeroDivisionError. By capturing the specific exception, we can handle the division by zero scenario in a more controlled fashion. This allows for cleaner and more readable code, as we explicitly mention the handling of divide by zero scenarios.
Now, let’s address some frequently asked questions related to the RuntimeWarning: divide by zero encountered in log:
### FAQs
Q1: What does the ‘divide by zero encountered in log’ warning mean?
A1: This warning message indicates that the code performed a logarithmic operation on a value that was either zero or less than zero (invalid inputs for logarithmic calculations).
Q2: How can I fix the RuntimeWarning: divide by zero encountered in log?
A2: To fix this warning, you can either add conditional statements to ensure that the denominator is greater than zero or utilize exception handling to capture and handle the ZeroDivisionError.
Q3: Is it necessary to handle this warning in my code?
A3: Handling this warning depends on the specific context of your code. It is generally a good practice to handle exceptions and warnings appropriately to maintain program stability and avoid unexpected crashes. However, the necessity may vary based on the specific requirements and logic of your code.
Q4: Can I suppress this warning without handling it explicitly?
A4: Yes, it is possible to suppress warnings using the `warnings` module in Python, specifically the `filterwarnings()` function. However, it is generally advisable to handle warnings instead of suppressing them, as it allows for better control and understanding of the code’s behavior.
In conclusion, the RuntimeWarning: divide by zero encountered in log is an important warning message that ensures mathematical operations are performed correctly in Python. By understanding the causes of this warning and implementing suitable solutions like conditional statements or exception handling, programmers can ensure their code executes without any unexpected mathematical inconsistencies.
Images related to the topic runtimewarning: overflow encountered in exp

Found 41 images related to runtimewarning: overflow encountered in exp theme





Article link: runtimewarning: overflow encountered in exp.
Learn more about the topic runtimewarning: overflow encountered in exp.
- How to Fix: RuntimeWarning: overflow encountered in exp
- How to Fix: RuntimeWarning: Overflow encountered in exp
- Overflow Error in Python’s numpy.exp function
- RuntimeWarning: overflow encountered in exp [Solved]
- Overflow Encountered in numpy.exp() Function in Python
- Overflow Encountered In Exp – MindMajix Community
See more: https://nhanvietluanvan.com/luat-hoc/