Discrete Value Supplied To Continuous Scale
Discrete Values and Continuous Scales are two fundamental concepts in statistics and data analysis. While discrete values refer to distinct and separate values, continuous scales represent a range of values without any gaps. Understanding the characteristics, measurement scales, and implications of both discrete and continuous data is essential for accurate data representation and analysis. In this article, we will explore the concept of discrete values, continuous scales, and how they relate to each other. We will also discuss common challenges, techniques for handling discrete values on continuous scales, statistical analysis, pitfalls, and future directions in this field.
Understanding Discrete Data
Discrete data consists of distinct and separate values that can only take on specific values within a defined set. These values are often counted or enumerated and cannot be divided into smaller intervals. Some common characteristics of discrete data include the fact that it is finite, countable, and can be expressed as whole numbers. Examples of discrete data include the number of siblings a person has, the number of cars in a parking lot, or the number of trees in a forest.
Measurement scales for discrete data include nominal and ordinal scales. Nominal scales assign categories or labels to data without any inherent order or ranking. For example, eye color (blue, brown, green) or blood type (A, B, AB, O) are nominal scales. On the other hand, ordinal scales represent data with a natural order or ranking, but the intervals between values may not be equal. Examples of ordinal scales include survey response scales (e.g., strongly disagree, disagree, neutral, agree, strongly agree) or education levels (e.g., elementary, middle, high school, college, graduate).
Exploring Continuous Data
Continuous data, in contrast to discrete data, can take on any value within a specific range or interval. It is not limited to distinct, separate values and can be measured or observed at any point on a continuous scale. Continuous data is characterized by its infinite nature, as it can take on an infinite number of values. Examples of continuous data include height, weight, temperature, or time.
Measurement scales for continuous data include interval and ratio scales. Interval scales represent equal differences between values, but the absence of a true zero point. Examples of interval scales include temperature (e.g., Fahrenheit or Celsius) or calendar year. Ratio scales, on the other hand, have equal intervals between values and a true zero point. Examples of ratio scales include age, income, or distance.
Discrete Values on Continuous Scales
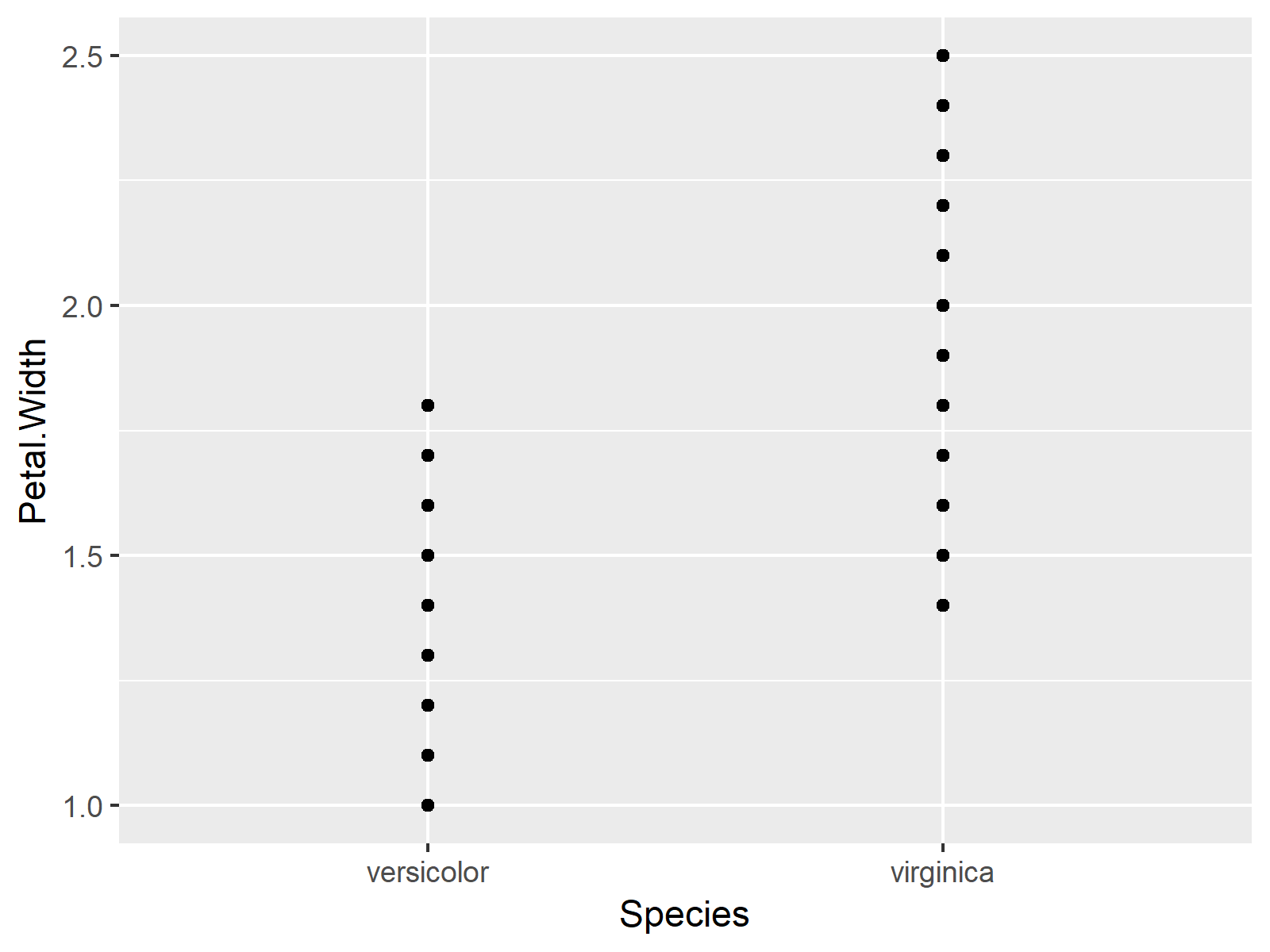
The concept of discrete values on continuous scales refers to the use of distinct and separate values within a range of continuous values. In some cases, discrete data can be plotted on a continuous scale, causing potential implications and challenges. For example, plotting data points with discrete values on a continuous scale can result in distorted representations or misleading interpretations.
Possible implications of using discrete values on continuous scales include the loss of precision, misrepresentation of data, and challenges in data analysis. When discrete values are forced onto a continuum, the true nature of the data may be compromised, leading to inaccurate conclusions or misleading visualizations. Additionally, treating discrete values as continuous can alter the statistical properties, such as the mean or variability, affecting further analysis.
Application of Discrete Values to Continuous Scales
Despite the challenges, there are situations where applying discrete values to continuous scales can be useful. Real-world examples include representing survey responses on a Likert scale as continuous values for statistical analysis or plotting counts of events over time as a continuous line graph. In such cases, the benefits of using continuous scales, such as smooth visualizations or enhanced statistical analysis, may outweigh the limitations.
Nevertheless, it is essential to consider the limitations of this approach. Discrete values on continuous scales may result in misleading interpretations, as the underlying discrete nature of the data may be concealed. Researchers and analysts must exercise caution and ensure that any conclusions drawn are contextually appropriate and accurately represent the nature of the data.
Techniques for Handling Discrete Values on Continuous Scales
To address the challenges posed by discrete values on continuous scales, several techniques can be employed:
1. Data Transformation: Transforming the data before plotting or analysis can help address the issues associated with discrete values on continuous scales. For example, taking the logarithm or square root of the discrete values can create a more suitable representation on a continuous scale.
2. Binomial and Ordinal Scales: Instead of representing discrete values on a continuous scale, using binomial or ordinal scales may provide a more appropriate representation. Creating grouped categories or ranks for discrete values can maintain the integrity of the data while still capturing valuable information.
3. Interpolation and Extrapolation: Interpolation involves estimating values between known data points, while extrapolation estimates values beyond the known data range. These techniques can be applied to fill in gaps or extend the range of discrete values on a continuous scale, providing a more comprehensive visualization or analysis.
Statistical Analysis with Discrete Values on Continuous Scales
When performing statistical analysis with discrete values on continuous scales, it is crucial to choose appropriate methods that account for the nature of the data.
Descriptive statistics, such as measures of central tendency (mean, median, mode) or measures of dispersion (variance, standard deviation), can still be applied to discrete values on continuous scales. These statistics provide a summary of the data and can help identify patterns or trends.
Inferential statistics, which involve making predictions or inferences about a population based on sample data, can be challenging with discrete values on continuous scales. Limitations such as the loss of precision or the distortion of the data’s actual distribution must be considered when applying inferential statistics.
Common Mistakes and Pitfalls
When dealing with discrete values on continuous scales, there are several common mistakes and pitfalls to avoid:
1. Incorrect Data Representation: Treating discrete values as continuous without considering the underlying nature of the data can lead to misleading representations or misinterpretations. It is essential to accurately represent the data and avoid distorting its properties.
2. Overlooking Discrete Values’ Impact: Failing to acknowledge and consider the impact of discrete values on continuous scales can result in biased or inaccurate analysis. The discrete nature of the data should be taken into account to ensure appropriate statistical methods are used.
Future Directions and Research Opportunities
Advancements in data collection and analysis are continually shaping the field of discrete values on continuous scales. Improvements in technology have allowed for more detailed and accurate data collection, expanding the possibilities for using discrete values on continuous scales.
Additionally, the development of new methods and techniques for handling discrete values on continuous scales can provide researchers and analysts with more reliable and robust tools. Exploring the potential of Geom_point, Pick scale, Scale_fill_discrete, Scale_y_continuous, Scale_fill_continuous, Scale_fill_brewer, Theme_bw, Scale_fill_manualdiscrete value supplied to continuous scale can lead to advancements in data representation and analysis.
In conclusion, understanding the relationship between discrete values and continuous scales is crucial for accurate data representation and analysis. While discrete data consists of distinct and separate values, continuous scales represent a range of values without gaps. Handling discrete values on continuous scales requires careful consideration to avoid misrepresentation and biased analysis. By employing appropriate techniques and statistical methods, researchers and analysts can derive meaningful insights from data with both discrete and continuous characteristics.
R Ggplot2 Error: Discrete Value Supplied To Continuous Scale (2 Examples) | How To Reproduce And Fix
What Does Discrete Value Supplied To Continuous Scale Mean?
In the field of mathematics and statistics, scales are often used to measure and represent data. Two common types of scales are the discrete scale and the continuous scale. While the discrete scale consists of separate and distinct values, the continuous scale allows for a limitless number of values within a given range. But what happens when a discrete value is supplied to a continuous scale? In this article, we will explore this concept in depth and provide a comprehensive understanding of what it means.
Understanding Discrete and Continuous Scales
Before diving into the topic, it is crucial to have a clear understanding of what discrete and continuous scales are.
A discrete scale, as the name suggests, is composed of separate and distinct values. These values are often whole numbers or categories that do not have intermediate values or decimal places. For example, when measuring the number of children in a family, the scale may consist of the values 0, 1, 2, 3, and so on. Each value represents a specific count and is not connected to other values on the scale.
On the other hand, a continuous scale contains infinite values within a given range. These values can take on any numeric value, and there are no gaps or interruptions between them. An example of a continuous scale is measuring the height of individuals. Heights can range from fractions of an inch to several feet, with no predetermined values.
Discrete Value Supplied to Continuous Scale
When a discrete value is supplied to a continuous scale, it means that a distinct and separate value from the discrete scale is used within the continuous scale. To better understand this concept, let’s consider an example.
Suppose we have a continuous scale representing the temperature in Celsius. The scale ranges from -10°C to 40°C, encompassing a variety of values. However, if we supply a discrete value to this scale, such as 30°C, it does not fit within the continuous nature of the scale. Discrete values do not have intermediate values, but a continuous scale allows for infinite possibilities.
Utilizing a discrete value on a continuous scale can cause several issues. For instance, it may disrupt the continuity of data representation and analysis. In the example given, if the temperature is measured and recorded as a continuous value, it allows for more accurate analysis, such as calculating an average temperature over a given time period. Supplying it as a discrete value does not provide the same level of accuracy and can introduce errors within the analysis.
FAQs
1. Why is it important to differentiate between discrete and continuous values?
Differentiating between discrete and continuous values is essential as it determines the appropriate scale and analysis techniques for a given dataset. Discrete values are typically counted and analyzed differently from continuous values, which can impact the interpretation of results.
2. Can a continuous value be used as a discrete value?
While it is technically possible to use a continuous value as a discrete value, it is uncommon and generally not considered best practice. Using a continuous value as a discrete value limits the precision and accuracy of data representation and can lead to misleading results.
3. How can one avoid using discrete values on continuous scales?
To avoid using discrete values on continuous scales, it is important to clearly define the nature of the data being measured. If the data is discrete, such as the number of children in a family, it should be represented on a discrete scale. However, if the data is continuous, such as height or temperature, it should be measured and recorded on a continuous scale.
In conclusion, the use of a discrete value on a continuous scale disrupts the continuity and accuracy of data representation and analysis. Discrete values are separate and distinct, while continuous scales allow for an infinite number of values within a range. It is important to differentiate between these two types of scales and use the appropriate one based on the nature of the data being measured. By understanding this concept, researchers and statisticians can ensure accurate and meaningful analysis of their data.
What Is The Error Continuous Value Supplied To Discrete Scale In A Map?
Maps serve as powerful tools for visualizing spatial data and conveying information effectively. Whether it is to represent geographic features, illustrate population densities, or showcase statistical information, maps enable us to perceive patterns, identify trends, and make informed decisions. However, when working with mapping software or creating our own maps, we may encounter a common error message: “Continuous value supplied to discrete scale.” In this article, we will delve into the meaning of this error and explore its implications in map making.
Understanding Scales in Maps:
Before diving into the error message itself, it is crucial to understand the concept of scales in maps. A map scale indicates the relationship between a distance on a map and the corresponding distance on the ground. It helps users comprehend the extent and proportions of the geographical area being represented. Scales can be classified into two major types: continuous scales and discrete scales.
1. Continuous Scale:
A continuous scale is used to represent data that falls on a continuous numerical range, usually with infinite values. In other words, the variable being visualized is uninterrupted and can assume any possible value within a given range. Examples of data suitable for continuous scales include temperature, elevation, precipitation, and population density.
2. Discrete Scale:
Unlike continuous scales, discrete scales are appropriate for representing data that falls into distinct categories or classes. Each class represents a mutually exclusive group, and the variables cannot assume any value in between. Examples of data suitable for discrete scales include categorical variables like land use types (forest, meadow, urban area), population groups (age groups, ethnicities), or any other attribute that can be divided into clear classes.
The Error: “Continuous Value Supplied to Discrete Scale”:
Now that we understand the basics of scales in maps, let’s explore the error message “Continuous value supplied to discrete scale.” This error occurs when we attempt to visualize a continuous variable using a map layer or graphic element that is defined as a discrete scale. Essentially, we are trying to represent a continuous range of values using distinct categories or classes. This discrepancy leads to conflict between the data and the map’s visual encoding.
Implications and Solutions:
When faced with the “Continuous value supplied to discrete scale” error, there are a few potential implications and suggested solutions to consider:
1. Misinterpreted Data: The error could arise from a misunderstanding of the nature of the data being visualized. Ensure that the variable you are trying to depict is indeed continuous and not discrete. Rethinking the data classification and identifying appropriate categorizations could help to resolve this issue.
2. Incorrect Scale Definition: Double-check your mapping software or settings to ensure that the appropriate scale type is being used for the data in question. If you are using a predefined map layer, verify that the scale definition matches the variable’s nature. Adjusting the scale definition may resolve the error.
3. Reassessing Visualization Techniques: Consider alternative ways of visualizing your continuous data. If a discrete scale is not suitable, explore options such as color gradients, proportional symbols, or choropleth maps, which are commonly used for continuous variables. Choosing a different visualization technique can prevent the error from occurring.
FAQs:
Q1. Why is it important to use the correct scale type?
A1. Using the correct scale type ensures that the data is accurately represented and prevents the “Continuous value supplied to discrete scale” error. It also allows users to interpret the information effectively and draw accurate conclusions from the map.
Q2. Can’t we just convert the data to fit the map scale?
A2. Converting a continuous variable to fit a discrete scale may result in a loss of information. In some cases, it might be possible to recode or aggregate the data, but this may not always be desirable or feasible. It is generally best to choose a visualization technique that aligns with the variable’s nature.
Q3. Are there any specific mapping software that avoid this error?
A3. Most modern mapping software applications, such as ArcGIS, QGIS, or Tableau, offer a range of scale options and allow users to define scales based on data characteristics. It is crucial to understand the capabilities and limitations of the software you are using to avoid this error.
Q4. What if my data has both discrete and continuous variables?
A4. If your data includes both discrete and continuous variables, you will need to choose appropriate visualization techniques for each variable. Ensure that the scales used correspond to the variable’s nature to avoid conflicts.
In conclusion, the error “Continuous value supplied to discrete scale” is a common obstacle encountered when visualizing continuous data using a discrete scale in maps. It signifies a mismatch between the nature of the data and the chosen scale. Understanding scales, double-checking settings, reevaluating data categorization, and exploring alternative visualizations can help resolve this error and create more accurate and informative maps.
Keywords searched by users: discrete value supplied to continuous scale Geom_point, Pick scale, Scale_fill_discrete, Scale_y_continuous, Scale_fill_continuous, Scale_fill_brewer, Theme_bw, Scale_fill_manual
Categories: Top 24 Discrete Value Supplied To Continuous Scale
See more here: nhanvietluanvan.com
Geom_Point
Understanding the basics of Geom_point is essential for effectively communicating and analyzing data. In this article, we will explore the concept of Geom_point in-depth, discussing its definition, key features, and how to use it for creating scatterplots. We will also address common misconceptions and provide a useful guide for beginners. So, let’s dive in!
Geom_point is a geometric object in the ggplot2 library, a comprehensive data visualization package in the R programming language. In simple terms, it refers to the points or markers on a scatterplot. It is worth mentioning that scatterplots display the relationship between two variables in a dataset. One variable is represented on the x-axis, while the other is represented on the y-axis. Each point on the scatterplot corresponds to a specific value of the two variables.
One of the key features of Geom_point is its ability to handle datasets with a large number of points efficiently. It allows users to plot thousands, or even millions, of data points without sacrificing performance. Moreover, it supports various customization options, including changing point size, shape, color, and transparency.
To make use of Geom_point, it is important to have some basic knowledge of the ggplot2 library. It follows a layered approach to data visualization, where each layer represents a specific component of the plot. Therefore, before using Geom_point, you need to create a basic plot using ggplot() and define aesthetic mappings to encode variables, such as aes(x = variable1, y = variable2). Then, you can add the Geom_point layer using the “+” operator, specifying any desired customization options.
Now, let’s discuss the steps involved in creating scatterplots using Geom_point. First, load the ggplot2 library in your R environment. Then, import your dataset and create a basic plot using ggplot(), specifying the variables you want to plot on the x and y-axes. For example, if you want to visualize the relationship between height and weight, you would use ggplot(data = your_data, aes(x = height, y = weight)).
Next, add the Geom_point layer using the “+” operator. By default, Geom_point will use a standardized set of values for the aesthetics, creating a scatterplot with default point shapes and sizes. However, you can customize these aesthetics to suit your preferences. For instance, you can change the point size by including the size parameter like geom_point(size = 3), where 3 represents the desired point size.
Similarly, you can modify other aesthetics, such as the point shape using the shape parameter, point color using the color parameter, and point transparency using the alpha parameter. There are various options available for these parameters, allowing you to create unique and visually appealing scatterplots.
In addition to basic geometric objects, Geom_point can also handle grouped scatterplots. Grouped scatterplots are useful for comparing the relationship between two continuous variables across different categories or groups. To create such plots, you need to specify an additional variable using the group parameter in the aes() function. This will assign different colors or shapes to the points based on the specified grouping variable, making it easier to differentiate between different categories in the scatterplot.
Now, let’s address some frequently asked questions (FAQs) about Geom_point.
FAQs:
Q: Can Geom_point handle missing values in the dataset?
A: Yes, Geom_point can handle missing values. By default, it will omit any missing values and create a scatterplot using the available data points.
Q: Is it possible to create scatterplot matrices using Geom_point?
A: Yes, scatterplot matrices can be created using the ggplot2 library, which includes Geom_point. By adding multiple Geom_point layers, each representing a different combination of variables, you can generate a matrix of scatterplots.
Q: Can I customize the appearance of the points individually?
A: Yes, you can customize the appearance of points individually by mapping specific aesthetics to variables in the dataset. For instance, you can map color to a categorical variable, resulting in different colored points based on the variable’s values.
Q: Are there any alternatives to Geom_point for creating scatterplots?
A: Yes, there are alternative geometric objects in the ggplot2 library, such as Geom_jitter and Geom_text, which can be used to create scatterplots with added functionalities like horizontal or vertical jittering or the display of text labels.
In conclusion, Geom_point is a versatile tool for creating scatterplots in data analysis and visualization. It allows users to represent data points on a plot, visualizing the relationship between two continuous variables. With its rich customization options and compatibility with the ggplot2 library, Geom_point provides an excellent tool for exploring and understanding datasets. So, give it a try, and unlock the immense power it offers in visualizing your data!
Pick Scale
Introduction:
The Pick Scale, also known as the Picking Scale, is a measuring system used by guitarists to describe the thickness or gauge of a guitar pick. The scale provides a standardized way to differentiate picks based on their thickness, thereby influencing the player’s tone, attack, and playability. In this article, we will explore the Pick Scale in detail, explaining its importance and how it affects your playing experience.
The Importance of Pick Thickness:
The thickness of a guitar pick affects various aspects of your playing, including tone, speed, and control. Thin picks generally produce a brighter and more treble-heavy sound, suitable for delicate strumming and intricate picking patterns. Conversely, thicker picks have a more substantial feel and produce a darker, bass-rich tone, well-suited for aggressive strumming and heavy playing styles. The choice of pick thickness is entirely subjective, and it usually depends on personal preference and musical genres.
Understanding the Pick Scale:
The Pick Scale is typically measured in millimeters (mm) or fractions of an inch. Picks with lower gauge measurements are thinner, while higher gauge measurements represent thicker picks. The most common thicknesses are generally labeled with the following gauges:
1. Extra Thin: Ranging from 0.38mm to 0.45mm, extra-thin picks are well-suited for acoustic players desiring a light touch and increased attack. These picks allow for swift picking and facilitate intricate fingerstyle playing.
2. Thin: Ranging from 0.46mm to 0.69mm, thin picks offer a versatile range of playing styles, suitable for both strumming and picking. They strike a balance between brightness and fullness of tone, making them popular among a wide array of guitarists.
3. Medium: Ranging from 0.70mm to 0.84mm, medium picks are ideal for players seeking a well-rounded tone with enhanced control. They offer a bit more resistance, making them suitable for heavy strumming and moderately aggressive playing styles.
4. Thick: Ranging from 0.85mm to 1.20mm, thick picks are favored by rock and metal guitarists due to their robust, dark tone and increased durability. These picks offer excellent control and are designed to withstand vigorous playing, making them a reliable choice for those seeking longevity.
5. Extra Thick: Ranging from 1.21mm and above, extra-thick picks are designed for the heaviest playing styles. They provide a powerful and full-bodied tone, aimed at generating maximum attack and sustain. Such picks are often preferred by heavy metal or hard rock guitarists looking to produce rich, aggressive sounds.
Common FAQs about the Pick Scale:
1. Are there any other scales used to measure pick thickness?
Yes, besides the Pick Scale, some manufacturers use their own proprietary systems to describe the thickness of their picks. However, the Pick Scale remains the most widely recognized and standardized method across the guitar industry.
2. Should beginners opt for thinner picks?
For beginners, it is recommended to start with a medium gauge pick. This allows for a reasonable amount of control while still offering some flexibility in playing styles. Experimenting with different picks is encouraged to find the one that feels most comfortable and suits your playing preferences.
3. Does pick thickness affect electric and acoustic guitars differently?
While the effect of pick thickness is generally consistent across both electric and acoustic guitars, it may be more noticeable on acoustics due to the guitar’s natural resonance. Additionally, thicker picks tend to produce a fuller sound on an acoustic, while thinner picks may emphasize string brightness.
4. How often do picks need to be replaced?
The longevity of a pick depends on various factors, including playing style and pick material. Thinner picks may wear down more quickly, especially when used for aggressive strumming, while thicker picks tend to be more durable. It is recommended to periodically inspect your picks for any signs of wear and tear and replace them as needed.
Conclusion:
The Pick Scale is an indispensable tool for guitarists, allowing for a nuanced selection of picks based on desired tonal characteristics and playing preferences. Understanding pick thickness and the various options available empowers players to tailor their sound and enhance their playing experience. Regardless of your preferred genre or playing style, the Pick Scale ensures that there is a perfect pick out there for you.
Scale_Fill_Discrete
Introduction (110 words):
In the field of data visualization, colors play a crucial role in conveying information effectively. They can aid in highlighting patterns, distinguishing categories, and emphasizing insights. One powerful tool in this domain is “scale_fill_discrete” from the R programming language. This function allows users to create visually stunning graphs and charts, with each variable category assigned a unique color. In this article, we will delve into the intricacies of scale_fill_discrete, exploring its functionalities, applications, and best practices. Additionally, we will address frequently asked questions to assist users in optimizing their data visualization endeavors.
I. What is scale_fill_discrete? (150 words)
At its core, scale_fill_discrete is a function in R that assists data scientists and analysts in assigning distinct colors to discrete variables, allowing for meaningful visual representations. Built on the ggplot2 package, this function provides a wide range of customizable color palettes, enabling users to match their data with the most appropriate colors.
II. How to employ scale_fill_discrete (220 words)
Using scale_fill_discrete is straightforward, thanks to its intuitive syntax. R users need to include the function within the ggplot2 framework and specify the desired color palette. By mapping a discrete variable to the “fill” aesthetic, the function will automatically assign distinct colors to each category. For instance, in a bar chart illustrating sales data by region, each region would be assigned a unique color.
III. Customizing color schemes (300 words)
One significant advantage of scale_fill_discrete is its ability to customize color schemes. R users can choose from built-in color palettes, such as RColorBrewer and viridis, or manually define their own color sets. This flexibility allows for the creation of visually appealing and informative visualizations.
Moreover, users can modify the order of colors in their schemes, ensuring that the most critical categories stand out. By specifying the order of the factors, users can control how colors are assigned and prioritize specific information.
Additionally, scale_fill_discrete offers the possibility of adjusting the color palette to suit colorblind individuals. By utilizing colorblind-friendly palettes, sensitive data visualization can remain inclusive and accessible to a broader audience.
IV. Best practices for color selection (200 words)
When utilizing scale_fill_discrete, it is essential to follow color selection best practices. Firstly, colors chosen should be visually distinguishable from one another, preventing any ambiguity in understanding the data. Utilizing color-related tools, such as ColorBrewer2.org or the ggthemes package, can aid in finding color schemes that are both visually appealing and informative.
Furthermore, consider the context in which the visualization is presented. Ensure that the chosen color scheme fits the theme and purpose of the data, contributing to an overall cohesive and meaningful representation.
FAQs:
1. Can I use scale_fill_discrete in other programming languages?
Unfortunately, scale_fill_discrete is specific to R and the ggplot2 package. Other programming languages and data visualization libraries may have similar functions, but they will differ in syntax and functionality.
2. How can I change the default colors assigned by scale_fill_discrete?
To modify the default colors, you can specify a different color palette using the “scale_fill_manual” function. This allows you to manually assign colors to specific categories.
3. Can I use scale_fill_discrete for continuous variables?
No, scale_fill_discrete is specifically designed for discrete variables. For continuous variables, you would use a different function like “scale_fill_gradient” or “scale_fill_continuous”.
Conclusion (85 words):
Scale_fill_discrete offers a powerful and versatile tool for creating meaningful and visually appealing data visualizations. By providing a wide array of customizable color schemes, this function empowers users to create engaging charts and graphs that enhance data comprehension. Whether adjusting the color order, creating custom palettes, or ensuring accessibility for colorblind individuals, scale_fill_discrete helps users make the most out of their data visualization endeavors. So, harness the power of scale_fill_discrete in R and transform your data into impactful visual stories.
Images related to the topic discrete value supplied to continuous scale

Found 46 images related to discrete value supplied to continuous scale theme


















Article link: discrete value supplied to continuous scale.
Learn more about the topic discrete value supplied to continuous scale.
- How To Fix The R Error: discrete value supplied to continuous …
- Plotting with ggplot2: “Error: Discrete value supplied to …
- How to Fix R Error: Discrete value supplied to continuous scale
- How to Fix R Error: Discrete value supplied to continuous scale
- R ggplot2 Error: Continuous value supplied to discrete scale (2 …
- R Coding Errors Suck: Continuous Value Supplied to Discrete Scale
- Discrete scale – Pointerpro
- R ggplot2 Error: Discrete Value Supplied to … – Statistics Globe
- How to Fix R Error: discrete value supplied to … – R-Lang
- Error: Continuous Value Supplied To Discrete Scale: How To Fix
- Discrete value supplied to continuous scale : r/rprogramming
- Fix: Error: Discrete value supplied to continuous scale
- annotate error: Discrete value supplied to continuous scale
See more: blog https://nhanvietluanvan.com/luat-hoc