Degrees Of Freedom: Exploring The Statistical Concept R

Degrees of Freedom in Statistics: Understanding the Statistical Concept

1. Introduction to Degrees of Freedom
Degrees of freedom (df) is a crucial statistical concept that plays a significant role in various analyses. It refers to the number of independent pieces of information that are available to estimate or determine certain parameters within a statistical model. In simpler terms, it represents the number of values that are free to vary in a sample or population, given certain constraints.

2. Degrees of Freedom in Univariate Analysis
a. Definition of Degrees of Freedom in Univariate Analysis
In univariate analysis, degrees of freedom represent the number of observations in the sample that are independent and free to vary after taking into account certain constraints or known information.

b. Calculation of Degrees of Freedom in Univariate Analysis
To calculate degrees of freedom in univariate analysis, subtract one from the total number of observations in the sample. For example, if you have a sample size of 50, the degrees of freedom would be 50 – 1 = 49.

c. Significance of Degrees of Freedom in Univariate Analysis
Degrees of freedom allow us to make accurate statistical inferences and determine the variability within a sample. They play a crucial role in calculating test statistics and determining the significance of results.

3. Degrees of Freedom in Bivariate Analysis
a. Definition of Degrees of Freedom in Bivariate Analysis
In bivariate analysis, degrees of freedom refer to the number of independent observations that are available to estimate or determine the relationship between two variables while considering certain constraints or known information.

b. Calculation of Degrees of Freedom in Bivariate Analysis
The calculation of degrees of freedom in bivariate analysis is dependent on the sample size and the number of variables being considered. It is generally calculated as (n-1) – (k-1), where n represents the sample size and k represents the number of variables.

c. Importance of Degrees of Freedom in Bivariate Analysis
Degrees of freedom play a significant role in determining the reliability and significance of relationships between variables in bivariate analysis. They allow us to determine the appropriate statistical tests and evaluate the precision of results.

4. Degrees of Freedom in Multivariate Analysis
a. Definition of Degrees of Freedom in Multivariate Analysis
In multivariate analysis, degrees of freedom represent the number of independent observations available to estimate or determine various parameters in a statistical model when considering multiple variables simultaneously.

b. Calculation of Degrees of Freedom in Multivariate Analysis
Calculating degrees of freedom in multivariate analysis is complex and depends on the specific statistical model being used. It often involves taking into account the number of variables, sample size, and the complexity of the model being analyzed.

c. Significance of Degrees of Freedom in Multivariate Analysis
Degrees of freedom help assess the model’s flexibility and determine the appropriate statistical tests in multivariate analysis. They are essential for estimating parameters accurately and obtaining reliable results.

5. Degrees of Freedom in Hypothesis Testing
a. Role of Degrees of Freedom in Hypothesis Testing
Degrees of freedom are crucial in hypothesis testing as they affect the choice of statistical tests and the interpretation of results. They determine the critical values and the distribution of test statistics.

b. Calculation of Degrees of Freedom in Hypothesis Testing
The calculation of degrees of freedom in hypothesis testing varies depending on the specific test being conducted. It involves considering sample sizes, number of variables, and any constraints imposed by the hypothesis being tested.

c. Interpretation of Degrees of Freedom in Hypothesis Testing
Interpreting degrees of freedom in hypothesis testing involves understanding the number of independent observations available to estimate or test the parameters of interest. Higher degrees of freedom generally indicate greater variability and more reliable results.

6. Degrees of Freedom in Regression Analysis
a. Definition of Degrees of Freedom in Regression Analysis
In regression analysis, degrees of freedom represent the number of independent observations available to estimate the regression coefficients and the overall fit of the model.

b. Calculation of Degrees of Freedom in Regression Analysis
The calculation of degrees of freedom in regression analysis depends on the number of variables, sample size, and the complexity of the regression model. Typically, degrees of freedom are calculated as the difference between the total sample size and the number of variables being considered.

c. Interpretation of Degrees of Freedom in Regression Analysis
Interpreting degrees of freedom in regression analysis allows us to evaluate the reliability and significance of regression coefficients and the overall fit of the model. Higher degrees of freedom suggest more reliable estimates and stronger evidence of relationships between variables.

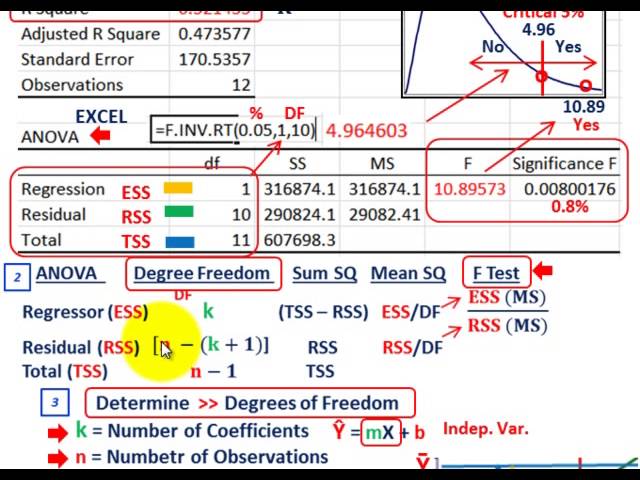
7. Degrees of Freedom in ANOVA (Analysis of Variance)
a. Definition of Degrees of Freedom in ANOVA
In ANOVA, degrees of freedom represent the number of independent observations available to estimate the variability between groups and within groups.

b. Calculation of Degrees of Freedom in ANOVA
The calculation of degrees of freedom in ANOVA involves considering the sample sizes of groups being compared and the total sample size. There are separate degrees of freedom for between-group and within-group variability.

c. Significance of Degrees of Freedom in ANOVA
Degrees of freedom in ANOVA play a crucial role in determining the significance of differences between groups. They are used to calculate test statistics and assess the reliability of results.

8. Degrees of Freedom in Chi-Square Test
a. Definition of Degrees of Freedom in Chi-Square Test
In the chi-square test, degrees of freedom represent the number of independent pieces of information available to estimate or test the observed and expected frequencies.

b. Calculation of Degrees of Freedom in Chi-Square Test
The calculation of degrees of freedom in the chi-square test depends on the number of categories being considered. It is calculated as the difference between the total number of categories and one.

c. Importance of Degrees of Freedom in Chi-Square Test
Degrees of freedom in the chi-square test help determine the appropriate test statistic and assess the significance of the observed frequencies. They allow us to evaluate the independence or association between categorical variables.

In conclusion, degrees of freedom are a fundamental concept in statistics that facilitate accurate estimation, testing, and interpretation of results across various analyses. Understanding the different types and calculations of degrees of freedom is vital to ensure valid statistical inferences.

How to Find Degrees of Freedom in R?

When working with statistical analysis, degrees of freedom play a crucial role in determining the validity and reliability of test results. In R, a powerful and popular programming language for statistical computing and graphics, finding degrees of freedom is a straightforward process. In this article, we will dive into the concept of degrees of freedom, explain how to calculate them, and provide some examples to reinforce the understanding. So, let’s get started!

Understanding Degrees of Freedom:
Degrees of freedom (df) refer to the number of independent pieces of information or values that are free to vary when estimating or testing statistical parameters. In simpler terms, it represents the number of values in a calculation that are allowed to vary or be chosen freely. Degrees of freedom help determine the appropriate distribution to use for hypothesis testing and confidence intervals. Generally, the formula for degrees of freedom is given by:

df = n – k

Where “n” represents the total number of observations in a dataset, and “k” represents the number of constraints or restrictions on those observations. Degrees of freedom are essential in various statistical tests, including t-tests, analysis of variance (ANOVA), chi-square tests, and regression.

Calculating Degrees of Freedom in R:
R, being a powerful statistical software, provides different functions to calculate degrees of freedom depending on the specific test or analysis being conducted. Below, we will explore how to find degrees of freedom for some common statistical tests in R.

1. T-Test:
The t-test is used to determine whether the mean of two groups is significantly different from each other. In R, the degrees of freedom for an independent two-sample t-test can be calculated using the following formula:

df = n1 + n2 – 2

Where “n1” and “n2” represent the sample sizes of the two groups being compared.

2. ANOVA:
Analysis of variance (ANOVA) assesses the differences between multiple group means. In R, the degrees of freedom for a one-way ANOVA can be calculated using the following formula:

df = n – k

Where “n” represents the total number of observations across all groups, and “k” represents the number of groups being compared.

3. Chi-Square Test:
Chi-square tests examine the association between categorical variables. In R, the degrees of freedom for a chi-square test can be calculated as:

df = (r – 1) * (c – 1)

Where “r” is the number of rows in the contingency table, and “c” is the number of columns.

4. Regression:
In regression analysis, degrees of freedom represent the number of independent observations available to estimate the parameters. In R, for simple linear regression, the degrees of freedom can be calculated as:

df = n – 2

Where “n” is the number of observations.

Frequently Asked Questions (FAQs):

Q1. How are degrees of freedom related to sample size?
A1. Degrees of freedom are indirectly related to sample size. As the sample size increases, the degrees of freedom tend to increase as well, providing more reliable and accurate statistical estimates.

Q2. Can degrees of freedom be negative?
A2. No, degrees of freedom cannot be negative. It represents the lower limit of variability for a given calculation.

Q3. Why are degrees of freedom important in statistical tests?
A3. Degrees of freedom help determine the appropriate distribution for hypothesis testing, ascertain the accuracy of parameter estimates, and avoid biased results. They enable researchers to draw conclusions from data with greater reliability.

Q4. Are degrees of freedom always whole numbers?
A4. In most cases, like the examples mentioned above, degrees of freedom are whole numbers as they represent the count of independent pieces of information. However, in some complex statistical models, degrees of freedom can take non-integer values.

Q5. How can I verify degrees of freedom in R?
A5. Many statistical functions or test outputs in R provide degrees of freedom as output. For example, when conducting a t-test in R, the output will include the degrees of freedom value.

Conclusion:
Degrees of freedom are a crucial component in statistical analysis, aiding in hypothesis testing, confidence intervals, and accurate parameter estimation. In R, calculating degrees of freedom depends on the specific statistical test being performed, such as t-tests, ANOVA, chi-square tests, or regression. By using the appropriate formulas and functions in R, you can easily determine the degrees of freedom for various analyses. Understanding and utilizing degrees of freedom correctly will enhance the validity and reliability of your statistical results.

Title: Understanding Degrees of Freedom: A Comprehensive Guide

Introduction:

Degrees of freedom (df) is a fundamental concept in statistics and research methodologies. It plays a crucial role in various statistical tests. Whether you are a student, researcher, or simply a curious individual looking to understand this concept, this article will provide an in-depth analysis of how to calculate degrees of freedom and its significance in statistical analysis.

Understanding Degrees of Freedom:

Degrees of freedom primarily refer to the number of independent pieces of information available in a sample or a statistical analysis. It represents the number of values that are free to vary in the calculation of a statistic. Different statistical tests require different formulas to determine the degrees of freedom, hence, it is essential to understand the concept for conducting accurate statistical analyses.

Common Methods to Calculate Degrees of Freedom:

1. One-sample t-test degrees of freedom:
In one-sample t-tests, degrees of freedom are calculated as (n – 1), where ‘n’ represents the number of observations in the sample. This formula allows for compensating for the reduction in information due to estimating the population mean.

2. Independent samples t-test degrees of freedom:
For independent samples t-tests, the degrees of freedom are found using a complex formula called the Welch-Satterthwaite formula. This formula considers the sample sizes and standard deviations of both groups and provides an accurate determination of the degrees of freedom for unequal samples.

3. Paired samples t-test degrees of freedom:
Paired samples t-tests assess the mean difference between two dependent groups. The degrees of freedom for these tests are simply the number of pairs minus one, represented as (n – 1).

4. Chi-square test degrees of freedom:
In a chi-square test of independence, the degrees of freedom are calculated based on the number of rows and columns in the contingency table. The formula for calculating the degrees of freedom is (r – 1) * (c – 1), where ‘r’ represents the number of rows and ‘c’ represents the number of columns.

Importance of Degrees of Freedom in Statistical Analysis:

Degrees of freedom play a vital role in statistical analyses and hypothesis testing. Statistical tests rely on degrees of freedom to determine the critical values and establish if the observed results are truly significant or occurred by chance alone. By understanding degrees of freedom, researchers can:

1. Determine the appropriate distribution to use: Degrees of freedom help identify the appropriate distribution, such as t-distribution or chi-square distribution, for performing statistical tests. Using an incorrect distribution can lead to erroneous conclusions.

2. Assess the variability within a dataset: Degrees of freedom allow researchers to account for the variability within a sample. The more degrees of freedom, the more reliable and precise the statistical tests become.

3. Avoid overfitting the data: Overfitting occurs when a statistical model is too complex and closely fitted to the dataset it was trained on. By considering the degrees of freedom, researchers can ensure that models and analyses are not excessively complex.

FAQs:

Q1. Are degrees of freedom always whole numbers?
No, degrees of freedom do not necessarily have to be whole numbers. In some statistical tests, such as regression, degrees of freedom can be fractional or decimal values.

Q2. What happens if I ignore degrees of freedom?
Ignoring degrees of freedom can lead to inaccurate conclusions and misinterpretation of statistical test results. It is crucial to account for degrees of freedom to obtain reliable and valid conclusions.

Q3. Can the degrees of freedom value ever be negative?
No, degrees of freedom cannot be negative. The lowest value degrees of freedom can take is zero, but this usually indicates that there is insufficient information to perform a particular statistical test.

Q4. How do I interpret degrees of freedom in research studies?
Interpreting degrees of freedom involves considering the number of independent observations available in a sample. A higher degree of freedom indicates a greater reliability in the statistical analysis and strengthens the validity of the conclusions.

Conclusion:

Degrees of freedom serve as a significant factor in statistical analyses, providing a measure of the variability and information available in a dataset. Understanding how to calculate degrees of freedom ensures accurate statistical tests and enhances the reliability of research findings. By grasping this concept, researchers can confidently utilize appropriate statistical tests, determine critical values, and interpret results accurately.

Degrees of Freedom Regression: Understanding the Statistical Concept

Introduction:

When it comes to performing a regression analysis, degrees of freedom play a crucial role in estimating the variability of our results and making accurate inferences. In statistical terms, degrees of freedom refer to the number of values that are free to vary in a statistical analysis, while still satisfying some specified constraint. In the context of regression analysis, degrees of freedom are used to determine the precision of our estimates and the validity of statistical tests. In this article, we will delve into the concept of degrees of freedom in regression, providing a comprehensive understanding of its significance and implications.

Understanding Degrees of Freedom in Regression Analysis:

In regression analysis, degrees of freedom specifically refer to the number of independent pieces of information that are available for estimating unknown parameters within a statistical model. It represents the number of observations minus the number of estimated coefficients or parameters in the model. The concept of degrees of freedom is closely tied to the idea that not all the information collected during the analysis can be used independently in estimating the unknown parameters.

Why is Degrees of Freedom Important in Regression?

Degrees of freedom play a pivotal role in regression analysis for several reasons:

1. Precision and Reliability: With a higher number of degrees of freedom, regression estimates tend to be more precise and reliable. As the number of degrees of freedom increases, we have more information available to estimate the coefficients, reducing the impact of random variation.

2. Validity of Statistical Tests: Degrees of freedom also determine the accuracy of statistical tests used in regression analysis. Statistical tests, such as t-tests and F-tests, rely on degrees of freedom to calculate critical values and determine the significance of the regression model. Insufficient degrees of freedom may lead to inaccurate or unreliable test results.

3. Overfitting and Model Complexity: Degrees of freedom are closely linked to the problem of overfitting in regression analysis. Overfitting occurs when a model becomes too complex and captures noise or random fluctuations in the data. Adequate degrees of freedom help prevent overfitting by ensuring that the model does not overly rely on every single data point.

Calculating Degrees of Freedom in Regression:

The calculation of degrees of freedom in regression analysis depends on the specific type of regression model being applied. In a simple linear regression model with one predictor variable, the degrees of freedom equation is:

df_regression = number of predictors

df_error = number of observations – number of predictors – 1

Here, “df_regression” corresponds to the degrees of freedom associated with the regression model, and “df_error” refers to the degrees of freedom associated with the residuals or error term. The subtraction of 1 in the “df_error” calculation accounts for the estimation of the intercept term.

For multiple regression models with more than one predictor variable, the degrees of freedom calculations become more complex. In general, the degrees of freedom for regression increase by the number of predictors used, while the degrees of freedom for error decrease accordingly.

Frequently Asked Questions (FAQs):

1. Can the degrees of freedom be negative in regression analysis?
No, degrees of freedom cannot be negative. The concept of degrees of freedom is based on the principle of constraint satisfaction, and it always results in a positive value.

2. How does the sample size affect degrees of freedom in regression analysis?
The sample size influences the degrees of freedom in regression analysis. Generally, as the sample size increases, the degrees of freedom for error increase, leading to more precise coefficient estimates and more accurate statistical tests.

3. What happens when there is a high degree of multicollinearity in regression analysis?
In situations where multicollinearity exists among predictor variables, the degrees of freedom for the predictors can decrease. Multicollinearity means that some predictor variables are highly correlated, leading to redundancy in information. As a result, the degrees of freedom for estimating the individual parameters decrease.

4. Are there any restrictions on the degrees of freedom for categorical predictor variables in regression analysis?
The number of degrees of freedom for categorical predictor variables is determined by the number of categories minus one. This is to avoid perfect collinearity. If all categories were included as predictors, one category would be a linear combination of the others, resulting in a loss of degrees of freedom.

Conclusion:

Degrees of freedom play a vital role in regression analysis, providing a means to estimate unknown parameters with precision and ensuring statistical tests’ accuracy. Understanding and correctly calculating degrees of freedom is crucial for sound statistical inference and interpretation of regression results. By grasping the concept of degrees of freedom in regression, researchers can enhance the reliability of their analyses and make informed decisions based on the data at hand.

Degrees of Freedom Formula: Explained and Examined

The concept of degrees of freedom is central to various areas of statistics, including hypothesis testing, chi-square tests, and t-tests. It is an essential tool that allows researchers to determine the reliability and accuracy of their statistical analysis. In this article, we will delve into the degrees of freedom formula, providing a comprehensive explanation and examining its significance in statistical analysis.

What are Degrees of Freedom?

Degrees of freedom (df) refer to the number of values in a calculation that are considered free to vary. In statistical terms, it represents the number of independent pieces of information that are used to estimate or determine a parameter. It is crucial to differentiate between the degrees of freedom for a population, which represents the number of independent values within the population, and the degrees of freedom for a sample, which accounts for the sample size.

Why is Degrees of Freedom Important?

The concept of degrees of freedom plays a fundamental role in statistical analysis by defining the appropriate distribution and critical values to use. Statistical tests, such as t-tests or chi-square tests, require specific degrees of freedom to compute accurate p-values and determine the statistical significance of the results. Neglecting to consider degrees of freedom can lead to erroneous conclusions and inaccurate estimations of variability.

Degrees of Freedom Formula

The degrees of freedom formula varies depending on the statistical test being conducted and the number of variables involved. Let’s explore some common scenarios:

1. One-Sample t-Test:
When conducting a one-sample t-test to compare the mean of a sample to a given population mean, the degrees of freedom formula is given by:
df = n – 1
Where ‘n’ represents the sample size.

2. Independent t-Test (Two-Sample t-Test):
When performing an independent t-test to compare the means of two independent groups, the degrees of freedom formula is given by:
df = n1 + n2 – 2
Where ‘n1’ and ‘n2’ represent the sample sizes of the two groups being compared.

3. Paired t-Test:
In a paired t-test, where observations are collected on the same sample at two different time points or under two different conditions, the degrees of freedom formula is:
df = n – 1
Again, ‘n’ denotes the number of pairs.

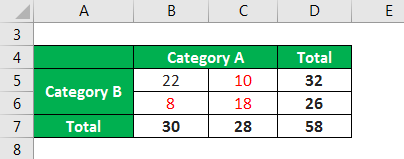
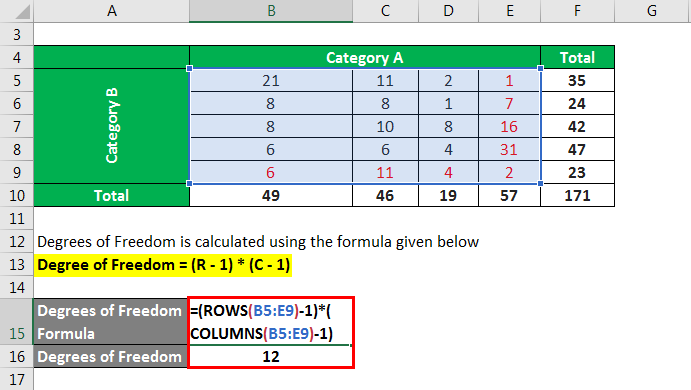
4. Chi-Square Test of Independence:
When conducting a chi-square test of independence to examine the relationship between two categorical variables, the degrees of freedom formula is given by:
df = (r – 1) * (c – 1)
Where ‘r’ represents the number of rows and ‘c’ represents the number of columns in the contingency table.

5. Analysis of Variance (ANOVA):
For a one-way ANOVA, which compares the means of three or more independent groups, the degrees of freedom formula is:
df = k – 1
Here, ‘k’ represents the number of groups being compared.

Frequently Asked Questions (FAQs)

Q1. Can degrees of freedom be negative?
No, degrees of freedom cannot be negative. Since it represents the number of independent values available for estimation or inference, it must always be a positive value.

Q2. Why do we subtract 1 when calculating degrees of freedom?
The subtraction of 1 when calculating degrees of freedom is based on the principle that one of the values used for estimation or inference is known, fixed, or determined. Subtracting 1 accounts for the restriction in variability caused by using this known value.

Q3. Can degrees of freedom exceed the sample size?
No, degrees of freedom cannot exceed the sample size. The maximum number of degrees of freedom is always equal to the sample size minus 1. It reflects the fact that one value in the sample is fixed, known, or determined.

Q4. What happens if we ignore degrees of freedom in statistical analyses?
Ignoring degrees of freedom in statistical analyses can lead to misleading and inaccurate results. It would result in incorrect p-values and invalid conclusions about the statistical significance of the findings. Proper consideration of degrees of freedom is crucial for accurate statistical inference.

In conclusion, the degrees of freedom formula is an integral part of statistical analysis, providing researchers with an essential tool to determine the reliability and significance of their findings. Understanding and correctly applying the appropriate degrees of freedom formula for various statistical tests is crucial for accurate estimation and inference. By paying attention to this concept, researchers can ensure their statistical analyses are robust and trustworthy.

Degrees of Freedom (n-2): Unraveling the Statistical Concept

When it comes to statistics, you may have come across the term “degrees of freedom.” It is a concept that plays a crucial role in various statistical analyses, such as t-tests, F-tests, and chi-square tests. Among the different formulas and equations encountered in statistical analysis, the phrase “n-2” often appears alongside degrees of freedom. In this article, we will explore the depths of degrees of freedom (n-2), explaining its meaning, significance, and providing answers to commonly asked questions.

What Are Degrees of Freedom?
In statistics, degrees of freedom represent the number of independent pieces of information available to estimate a statistic or parameter. It determines the number of values that are free to vary once certain restrictions are imposed. In simpler terms, it refers to the number of data points that are allowed to vary in a statistical analysis.

Degrees of Freedom (n-2):
The “n-2” component refers to the specific formula used to calculate degrees of freedom in a linear regression. In this case, “n” represents the sample size, i.e., the number of data points collected, while “2” signifies the number of parameters estimated in a linear regression analysis. These parameters are the slope and intercept of the regression line. Hence, degrees of freedom (n-2) indicate the number of independent observations available after estimating these two parameters.

Significance of Degrees of Freedom (n-2):
Degrees of freedom (n-2) are particularly crucial in linear regression analysis. The regression line represents the best-fit line that describes the relationship between two variables. To estimate this line accurately, degrees of freedom must be considered. By accounting for the number of parameters estimated, degrees of freedom (n-2) help adjust the statistical analysis, ensuring accurate and reliable results.

When determining the significance of degrees of freedom (n-2), remember that the larger the value, the more representative and reliable the statistical analysis. Higher degrees of freedom provide a greater number of independent observations, thus reducing the margin of error and increasing the accuracy of the estimates.

FAQs About Degrees of Freedom (n-2):

Q: Is degrees of freedom always equal to (n-2)?
A: No, degrees of freedom depend on the statistical analysis being performed. In many cases, it may indeed equal (n-2) if estimating two parameters. However, it can differ in other statistical methods, such as t-tests or chi-square tests.

Q: What happens if degrees of freedom are too low?
A: When degrees of freedom are too low, the statistical analysis becomes less accurate and reliable. This is because insufficient independent observations may lead to an inadequate representation of the population.

Q: Can degrees of freedom be negative?
A: No, degrees of freedom can only be positive or zero.

Q: Are there any limitations to degrees of freedom (n-2)?
A: Degrees of freedom (n-2) are ideal for linear regression analysis but may not be applicable or relevant in other statistical tests. Different tests have their own specific formulas to determine degrees of freedom.

Q: How are degrees of freedom estimated or calculated in more complex statistical analyses?
A: The calculation of degrees of freedom becomes more intricate in complex statistical tests. In such cases, consult the specific formula provided in the statistical method being used or refer to statistical software that automatically calculates degrees of freedom.

Q: Can degrees of freedom impact the interpretation of statistical results?
A: Yes, degrees of freedom play a crucial role in hypothesis testing and interpreting statistical results. They help determine the critical values for statistical tests and affect the calculation of p-values, confidence intervals, and hypothesis rejections or acceptances.

Q: How can degrees of freedom (n-2) be generalized to other degrees of freedom formulas?
A: Degrees of freedom depend on the specific statistical analysis being conducted. While “n-2” is applicable for simple linear regression, it would be different for other scenarios. The key is to understand the formula relevant to the statistical method you are using.

Degrees of freedom (n-2) hold significant importance in statistical analysis, especially in linear regression. By considering the number of parameters estimated when calculating degrees of freedom, accurate and reliable statistical results can be obtained. Understanding this concept allows researchers and analysts to draw more informative conclusions from their data and make sound statistical inferences.

Found 38 images related to degrees of freedom r theme