Boulter Coordinate Distance Calculator
The Boulter Coordinate Distance Calculator is a tool used to calculate the distance between two coordinates. It is commonly used in various fields such as geography, mathematics, navigation, and computer science. This calculator takes the latitude and longitude of two points and determines the distance between them.
How does the Boulter Coordinate Distance Calculator work?
The Boulter Coordinate Distance Calculator uses a mathematical formula called the Haversine formula to calculate the distance between two points on the Earth’s surface. This formula takes into account the curvature of the Earth, making it more accurate than simple straight-line calculations.
The Haversine formula is based on the principles of spherical trigonometry. It calculates the great-circle distance between two points on the surface of a sphere using their latitude and longitude. The great-circle distance is the shortest distance between two points on the surface of a sphere, and it represents the actual distance between the two points.
Benefits of using the Boulter Coordinate Distance Calculator
1. Accuracy: The Boulter Coordinate Distance Calculator provides accurate distance calculations, taking into consideration the Earth’s curvature. This accuracy is crucial in various applications such as navigation and geographical analysis.
2. Versatility: The calculator can be used with any set of coordinates, making it a versatile tool that can be applied to different scenarios. Whether you need to calculate the distance between two cities or two points on a map, the Boulter Coordinate Distance Calculator can handle it.
3. User-friendly interface: The Boulter Coordinate Distance Calculator is designed with a user-friendly interface, allowing users to input the coordinates easily and obtain the results quickly. Even those with limited technical knowledge can use this calculator without any difficulty.
4. Time-saving: By using the Boulter Coordinate Distance Calculator, users can save time by avoiding manual distance calculations or complex mathematical formulas. This tool provides instant and accurate results, thereby increasing efficiency in various tasks.
Limitations of the Boulter Coordinate Distance Calculator
1. One-dimensional distance: The Boulter Coordinate Distance Calculator only calculates the two-dimensional distance between two points on the Earth’s surface. It does not consider factors such as elevation or slope. For advanced applications that require three-dimensional distance calculations, additional tools or formulas may be necessary.
2. Limited to Earth coordinates: The Boulter Coordinate Distance Calculator is specifically designed for calculating distances on the Earth’s surface using latitude and longitude coordinates. It may not be suitable for calculating distances in other contexts or using different coordinate systems.
Practical applications of the Boulter Coordinate Distance Calculator
1. Navigation: The Boulter Coordinate Distance Calculator is commonly used in navigation systems and GPS devices. It helps determine the distance between the current location and a desired destination, aiding in route planning and navigation.
2. Geographical analysis: Geographers and researchers often use the Boulter Coordinate Distance Calculator to analyze geographical patterns and relationships. By calculating distances between various locations, they can uncover spatial trends and make informed decisions based on these findings.
3. Logistics and transportation: The Boulter Coordinate Distance Calculator plays a crucial role in logistics and transportation planning. It helps estimate travel distances, optimize routes, and determine fuel consumption, contributing to cost-effective and efficient transportation operations.
Comparison of the Boulter Coordinate Distance Calculator with other distance calculators
While there are various distance calculators available, the Boulter Coordinate Distance Calculator stands out due to its accuracy and ease of use. Compared to simple straight-line calculations, the Boulter Coordinate Distance Calculator takes into account the Earth’s curvature, providing more precise results. Additionally, its user-friendly interface makes it accessible to a wide range of users.
Future developments and improvements of the Boulter Coordinate Distance Calculator
As technology continues to advance, there are possibilities for future developments and improvements of the Boulter Coordinate Distance Calculator. Some potential areas for enhancement include:
1. Integration with other technologies: The Boulter Coordinate Distance Calculator could be integrated with other technologies, such as GIS (Geographic Information System), to provide more advanced spatial analysis capabilities.
2. Real-time data updates: The calculator could be enhanced to provide real-time updates, incorporating live data on traffic conditions, road closures, and other factors that affect distance calculations.
3. Enhanced visualization: Future versions of the Boulter Coordinate Distance Calculator could incorporate more advanced and interactive visualizations, allowing users to visualize distances on maps or virtual globes.
In conclusion, the Boulter Coordinate Distance Calculator is a valuable tool that provides accurate distance calculations between two coordinates. Its accuracy, versatility, and user-friendly interface make it a preferred choice for professionals in various fields. While the calculator has limitations, such as its focus on two-dimensional distances and Earth coordinates, it remains a valuable asset in navigation, geographical analysis, and transportation planning. With potential future developments, the Boulter Coordinate Distance Calculator is likely to continue evolving to meet the needs of its users.
FAQs
1. How do I calculate the distance between two coordinates using the Boulter Coordinate Distance Calculator?
To calculate the distance between two coordinates using the Boulter Coordinate Distance Calculator, enter the latitude and longitude of both points into the calculator. The result will be displayed as the distance between the two points.
2. Can I use the Boulter Coordinate Distance Calculator with any coordinate system?
The Boulter Coordinate Distance Calculator is specifically designed for calculating distances using latitude and longitude coordinates on the Earth’s surface. While it may not be suitable for other coordinate systems, there are other calculators available for different contexts.
3. Can the Boulter Coordinate Distance Calculator calculate three-dimensional distances?
No, the Boulter Coordinate Distance Calculator is designed to calculate two-dimensional distances between two points on the Earth’s surface. For three-dimensional distance calculations, additional tools or formulas may be required.
4. Is the Boulter Coordinate Distance Calculator accurate?
Yes, the Boulter Coordinate Distance Calculator is known for its accuracy. It uses the Haversine formula, which takes into account the Earth’s curvature, making it more accurate than simple straight-line calculations.
5. Can I use the Boulter Coordinate Distance Calculator for driving directions?
The Boulter Coordinate Distance Calculator calculates the straight-line distance between two points on the Earth’s surface. It does not provide driving directions or consider factors such as road networks or traffic conditions. For driving directions, it is recommended to use specialized navigation systems or mapping services that offer route planning functionalities.
Find Distance Between 2 Coordinates | Find Distance Between Coordinates In Excel
Keywords searched by users: boulter coordinate distance calculator Calculate distance between two coordinates, How to calculate distance between two points, Vector3 distance calculator, Get distance between two points Google Maps API, Euclidean distance calculator, Calculate distance between two coordinates Java, Calculate bearing between two coordinates, Calculate distance between two coordinates C#
Categories: Top 39 Boulter Coordinate Distance Calculator
See more here: nhanvietluanvan.com
Calculate Distance Between Two Coordinates
Calculating the distance between two coordinates is a fundamental concept in mathematics and geography. It allows us to determine the distance between two points on the earth’s surface or any other coordinate system. This article will guide you through the process of calculating the distance between two coordinates and provide answers to frequently asked questions.
To calculate the distance between two coordinates, we need to first understand latitude and longitude. Latitude represents the north-south position on the earth’s surface, while longitude represents the east-west position. Both latitude and longitude are measured in degrees.
One of the most common methods used to calculate the distance between two coordinates is the Haversine formula. This formula takes into account the Earth’s spherical shape and provides a more accurate result than simple Euclidean distance calculations.
The formula is as follows:
a = sin²(Δφ/2) + cos φ1 * cos φ2 * sin²(Δλ/2)
c = 2 * atan2(√a, √(1−a))
d = R * c
Where φ1, λ1 and φ2, λ2 are the latitude and longitude of two points respectively, Δφ = φ2 – φ1 and Δλ = λ2 – λ1. R is the radius of the Earth, which is approximately 6,371 kilometers.
Let’s go through an example to illustrate how the formula works. Suppose we have two coordinates: point A with latitude 40.7128° N and longitude 74.0060° W, and point B with latitude 34.0522° N and longitude 118.2437° W.
Using the Haversine formula, we can calculate the distance between these two points:
Δφ = 34.0522° – 40.7128° = -6.6606°
Δλ = 118.2437° – 74.0060° = 44.2377°
a = sin²(-6.6606°/2) + cos(40.7128°) * cos(34.0522°) * sin²(44.2377°/2)
c = 2 * atan2(√a, √(1−a))
d = 6371 * c
After plugging in the values and performing the calculations, we find that the distance between these two points is approximately 3,970 kilometers.
FAQs:
Q: What is the purpose of calculating the distance between two coordinates?
A: Calculating the distance between two coordinates is essential for numerous applications such as navigation systems, air travel planning, and logistics management. It helps determine the most efficient routes, estimate travel time, and optimize resource allocation.
Q: Is the Haversine formula the only method to calculate distance?
A: No, there are other methods available to calculate distance between two coordinates. The Vincenty formula is another popular method that provides a higher accuracy when calculating distances over long distances. However, for most everyday calculations, the Haversine formula suffices.
Q: Can the distance between two points be calculated using online tools or applications?
A: Yes, there are various online tools and applications available that can calculate the distance between two coordinates. These tools often provide additional features, such as the ability to calculate driving or walking distances, elevation changes, and more.
Q: How do I convert coordinates in degrees to radians for the Haversine formula?
A: To convert coordinates from degrees to radians, simply multiply the value by π/180. This conversion is necessary because most trigonometric functions operate on radians rather than degrees.
Q: Can the distance between two coordinates be negative?
A: No, the distance between two coordinates is always a positive value. The negative sign in the calculations represents the direction relative to a chosen reference point.
In conclusion, calculating the distance between two coordinates is an important mathematical concept used in various fields. The Haversine formula provides an accurate estimation of distance, taking into account the spherical shape of the Earth. Numerous online tools and applications simplify the calculations, allowing users to determine distances and plan travel efficiently.
How To Calculate Distance Between Two Points
In mathematics, calculating the distance between two points in a plane is a fundamental process used in various fields such as geometry, physics, and engineering. Whether you need to determine the distance between two cities on a map or measure the displacement of an object, knowing how to calculate distance accurately is essential. This article will explain the different methods to calculate the distance between two points and provide step-by-step instructions for each method.
Method 1: The Distance Formula
The most common method used to calculate the distance between two points in a plane is the Distance Formula. This formula is derived from the Pythagorean theorem and applies to any two-dimensional space.
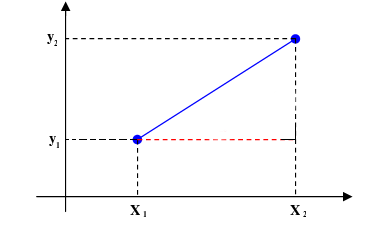
To find the distance between two points, represented as (x1, y1) and (x2, y2), follow these steps:
Step 1: Identify the coordinates of both points. Let’s say we have point A with coordinates (x1, y1) and point B with coordinates (x2, y2).
Step 2: Subtract the x-coordinates of the two points. (x2 – x1)
Step 3: Square the result obtained in step 2. (x2 – x1)^2
Step 4: Repeat steps 2 and 3, but this time subtracting the y-coordinates. (y2 – y1)^2
Step 5: Add the results obtained in step 3 and step 4. (x2 – x1)^2 + (y2 – y1)^2
Step 6: Take the square root of the result obtained in step 5. √((x2 – x1)^2 + (y2 – y1)^2)
By following these steps, you can calculate the distance between any two points in a plane using the Distance Formula.
Method 2: The Midpoint Formula
Sometimes, you may not need to find the distance between two points but rather the midpoint between them. The Midpoint Formula allows you to calculate the exact point that lies exactly in the middle of two given points.
To find the midpoint between two points, follow these steps:
Step 1: Identify the coordinates of both points, (x1, y1) and (x2, y2).
Step 2: Add the x-coordinates of the two points and divide the result by 2. [(x1 + x2)/2]
Step 3: Add the y-coordinates of the two points and divide the result by 2. [(y1 + y2)/2]
Step 4: The midpoint is represented as the coordinates obtained in step 2 and step 3. The midpoint is (∆x, ∆y), where ∆x = [(x1 + x2)/2] and ∆y = [(y1 + y2)/2].
By utilizing the Midpoint Formula, you can pinpoint the exact location that is equidistant from two given points.
FAQs:
1. Can I use these formulas in three-dimensional space?
The formulas provided above are specifically designed for two-dimensional space. However, in three-dimensional space, you can modify these formulas to account for an additional coordinate (z). In the Distance Formula, the expression [(x2 – x1)^2 + (y2 – y1)^2] can be expanded as [(x2 – x1)^2 + (y2 – y1)^2 + (z2 – z1)^2] to calculate the distance in three dimensions.
2. How accurate are these formulas?
The distance formulas explained here provide accurate results and can be used in various scenarios. However, it is important to ensure that the coordinates of the points are entered correctly, as any errors will impact the accuracy of the calculated distance.
3. Can these formulas be applied to calculate the distance between cities on a map?
Yes, these formulas can be used to calculate the distance between cities on a map. However, you must convert the latitude and longitude coordinates of the cities into Cartesian coordinates (x, y) before applying the formulas. Various online tools and software applications are available to assist in this conversion.
4. Is there any programming language or software that can automate this calculation?
Yes, many programming languages such as Python, Java, and C++ offer libraries and functions that automate the calculation of distances between two points. These libraries use variations of the formulas discussed above to perform the calculation efficiently.
In conclusion, calculating the distance between two points is a basic yet essential process in various mathematical disciplines. By applying the Distance Formula or the Midpoint Formula, you can accurately find the distance between any two points in a plane or locate the midpoint between them. Remember to verify the inputs and convert coordinates correctly when working in different dimensions or calculating distances on a map.
Vector3 Distance Calculator
Introduction:
A Vector3 distance calculator is a powerful tool used in various scientific and engineering fields to determine the distance between two points represented in a three-dimensional Cartesian coordinate system. This tool utilizes mathematical algorithms to calculate distances accurately and efficiently. In this article, we will delve deep into the workings of a Vector3 distance calculator, its applications, and potential FAQs to provide readers with a comprehensive understanding of this essential tool.
Understanding Vector3 Distance:
In mathematics, a vector represents a magnitude and direction in a specific coordinate system. In a three-dimensional Cartesian coordinate system, a Vector3 consists of three components: X, Y, and Z. These components represent positions in the x, y, and z directions, respectively. To calculate the distance between two Vector3 points, we use the Pythagorean theorem, which states that the square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides. In a three-dimensional space, this theorem can be extended to calculate the distance between two points.
To illustrate the calculation, let’s consider two Vector3 points p1 (x1, y1, z1) and p2 (x2, y2, z2). The formula to calculate the distance (d) between these two points is:
d = √((x2 – x1)^2 + (y2 – y1)^2 + (z2 – z1)^2)
This formula derives from applying the Pythagorean theorem in three dimensions. By substituting the respective coordinates of the points, we can easily calculate the distance between them. It is important to note that the distance is always positive and represents the shortest length between the two points.
Applications of Vector3 Distance Calculators:
1. Computer Graphics: Vector3 distance calculators are extensively used in computer graphics to create lifelike three-dimensional objects and scenes. By calculating distances between points, various effects such as lighting, shadows, and object interactions can be simulated accurately.
2. Robotics: In the field of robotics, Vector3 distance calculators play a crucial role. They enable robots to navigate their surroundings, avoid obstacles, and accurately determine the distance between their current position and a target destination.
3. Physics and Engineering: Vector3 distance calculation is fundamental in physics and engineering to analyze and solve problems related to motion, velocity, acceleration, and force. By accurately calculating distances, scientists and engineers can determine the optimal paths for objects and evaluate physical phenomena.
4. Gaming: In the gaming industry, Vector3 distance calculators are utilized to create realistic virtual environments. They enable the manipulation of game objects’ positions, ensuring precise collisions, accurate movement, and realistic physics simulations.
Frequently Asked Questions (FAQs):
1. Can a Vector3 distance calculator measure distances in any unit?
No, a Vector3 distance calculator calculates distances purely based on the coordinate values provided. However, it can work with any unit of measurement, as long as consistency is maintained throughout the calculation. It is advisable to use the same unit for all three coordinates to receive accurate distance results.
2. Is there a difference between Euclidean distance and Vector3 distance?
Euclidean distance is a term commonly used to describe the straight-line distance between two points. In a two-dimensional plane, Euclidean distance and Vector3 distance are the same since the z-component is zero. However, in three-dimensional space, the Vector3 distance considers all three dimensions, while the Euclidean distance only accounts for two dimensions.
3. Is there an alternative formula to calculate Vector3 distance?
No, the formula mentioned earlier (d = √((x2 – x1)^2 + (y2 – y1)^2 + (z2 – z1)^2)) is the standard formula used to calculate the Vector3 distance. It provides accurate results by calculating the square root of the sum of the square differences of each component.
4. Can a Vector3 distance calculator handle points represented in different coordinate systems?
No, a Vector3 distance calculator specifically works with points represented in a three-dimensional Cartesian coordinate system. Points represented in other coordinate systems, such as polar coordinates or cylindrical coordinates, would require conversion to the Cartesian system before using the distance calculator.
5. How can I implement a Vector3 distance calculator in my own code?
Implementing a Vector3 distance calculator depends on the programming language you are using. Most programming languages have built-in libraries or functions to calculate distances between points. By supplying the appropriate coordinates as inputs to the library or function, you can easily calculate the Vector3 distance.
Conclusion:
Vector3 distance calculators are invaluable tools in various scientific and engineering domains. By utilizing mathematical algorithms, these calculators accurately determine the distance between points represented in a three-dimensional Cartesian coordinate system. They find applications in fields such as computer graphics, robotics, physics, engineering, and gaming. Understanding the fundamentals of Vector3 distance calculation empowers professionals to leverage this tool effectively in their work.
Images related to the topic boulter coordinate distance calculator

Found 43 images related to boulter coordinate distance calculator theme

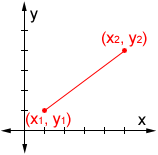



Article link: boulter coordinate distance calculator.
Learn more about the topic boulter coordinate distance calculator.
- Distance Between Cities – GPS Coordinates
- Latitude/Longitude Distance Calculator
- boulter.com Market Share, Revenue and Traffic Analytics
- The Road to Dawn: Josiah Henson and the Story That Sparked …
- How to Calculate distance between 2 sets of GPS coordinates
See more: https://nhanvietluanvan.com/luat-hoc/