Haskell Length Of List
Haskell is a powerful and purely functional programming language known for its strong type system and elegant syntax. One of the fundamental data structures in Haskell is the list, which can be defined as an ordered collection of elements. Lists can contain elements of any data type, such as integers, characters, or even other lists.
In Haskell, lists are defined using square brackets and separating the elements with commas. For example, [1, 2, 3] is a list containing the integers 1, 2, and 3. Lists can also be concatenated using the ++ operator, e.g., [1, 2, 3] ++ [4, 5] results in [1, 2, 3, 4, 5].
Understanding the Length Function in Haskell
The length function in Haskell is used to determine the number of elements in a list. It takes a list as input and returns an integer representing the length of the list. For example, applying the length function to the list [1, 2, 3] will yield 3, as it contains three elements.
Implementing the Length Function Using Recursion in Haskell
The length function can be implemented in Haskell using recursion. Here is an example implementation:
“`haskell
length :: [a] -> Int
length [] = 0
length (_:xs) = 1 + length xs
“`
In this implementation, we define a function named length that takes a list as input and returns an integer. The function uses pattern matching to handle two cases: an empty list and a list with at least one element. If the input list is empty ([]), the function returns 0. Otherwise, it recursively calls itself with the tail of the list (xs) and adds 1 to the result.
Analyzing the Time Complexity of the Length Function in Haskell
The time complexity of the length function implemented using recursion in Haskell is O(n), where n is the number of elements in the input list. This is because the function needs to traverse the entire list recursively to determine its length. Therefore, the running time of the length function is directly proportional to the size of the list.
Exploring the Space Complexity of the Length Function in Haskell
The space complexity of the length function implemented using recursion in Haskell is O(n), where n is the number of elements in the input list. This is because the function creates a new stack frame for each recursive call, consuming additional memory. Therefore, the space usage of the length function grows linearly with the size of the list.
Comparing the Length Function with Other List Manipulation Functions in Haskell
The length function is just one of many useful list manipulation functions available in Haskell. Here are some other commonly used functions:
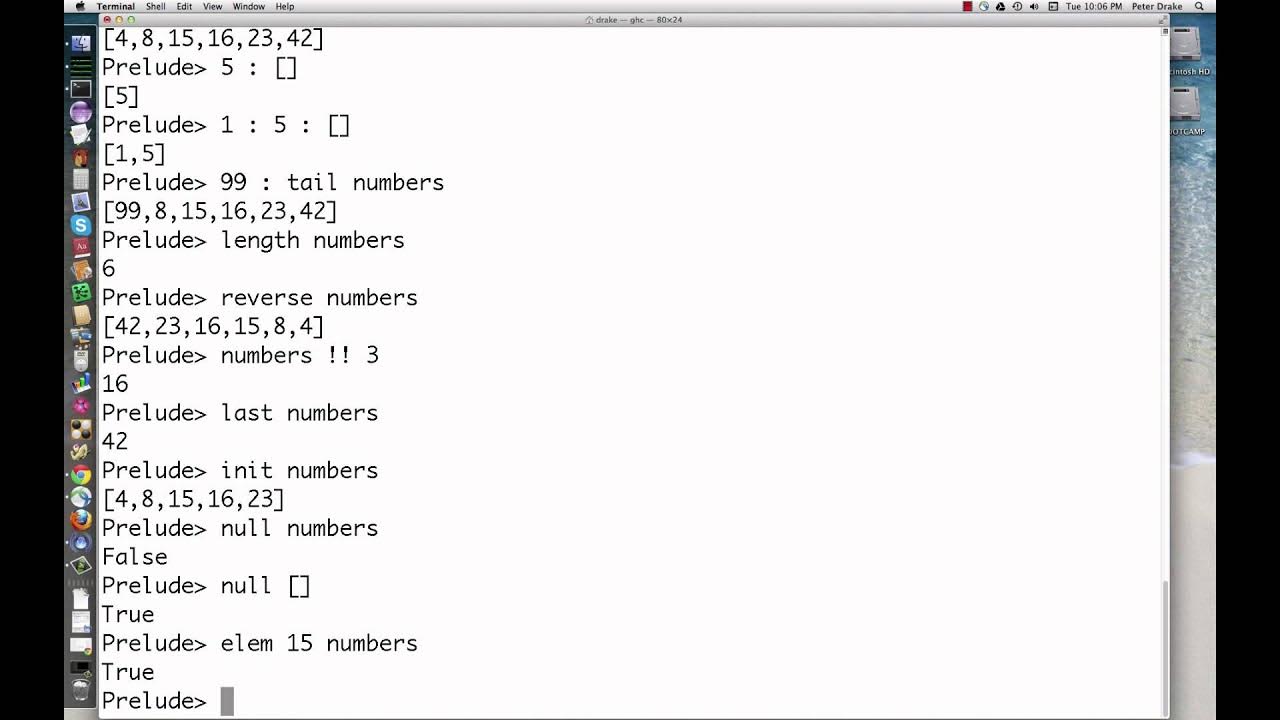
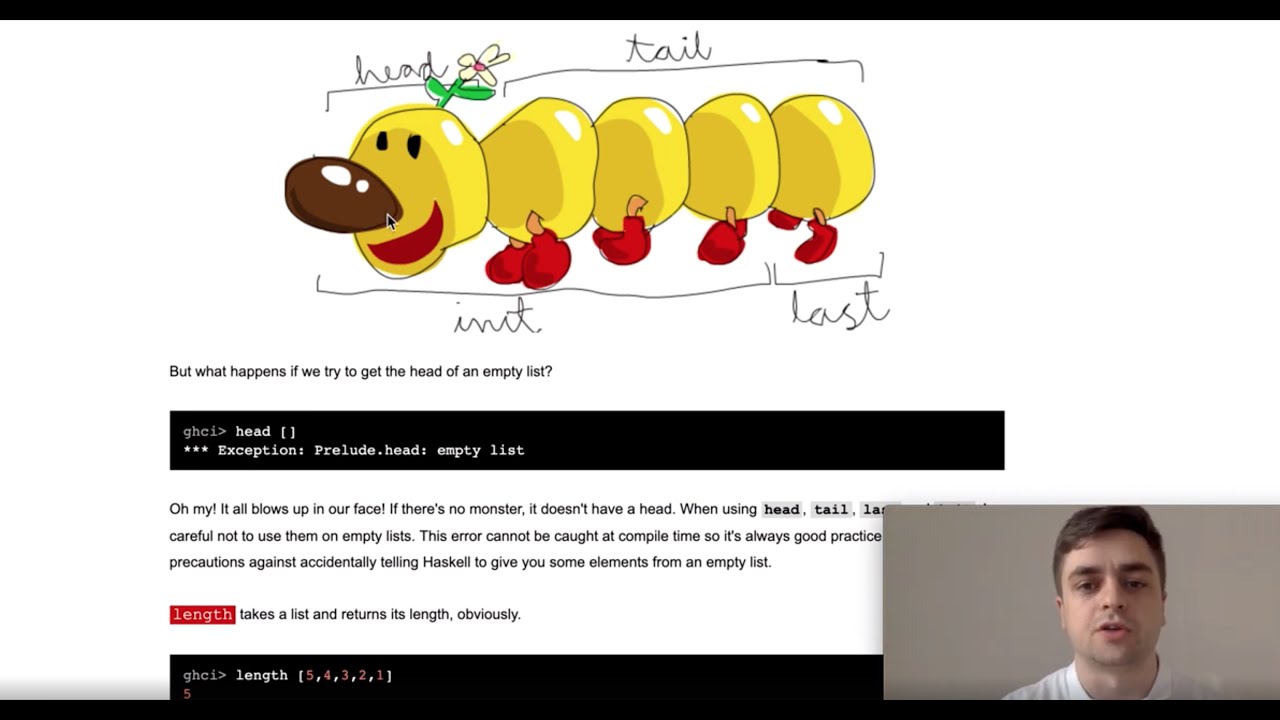
– `last` returns the last element of a list, e.g., `last [1, 2, 3]` returns 3.
– `splitAt` splits a list into two parts at a given position, e.g., `splitAt 2 [1, 2, 3, 4, 5]` returns `([1, 2], [3, 4, 5])`.
– `chunksOf` splits a list into chunks of a specified length, e.g., `chunksOf 2 [1, 2, 3, 4, 5]` returns `[[1, 2], [3, 4], [5]]`.
– `elemIndex` finds the index of the first occurrence of an element in a list, e.g., `elemIndex 2 [1, 2, 3]` returns `Just 1`.
– `delete` removes the first occurrence of an element from a list, e.g., `delete 2 [1, 2, 3]` returns `[1, 3]`.
– `null` checks if a list is empty, e.g., `null []` returns `True`.
Practical Applications and Examples of Using the Length Function in Haskell
The length function has various practical applications in Haskell programming. Here are some examples:
1. Computing the average of a list of numbers:
“`haskell
average :: [Double] -> Double
average xs = sum xs / fromIntegral (length xs)
“`
In this example, the length function is used to determine the number of elements in the list, which is then used to compute the average.
2. Checking if a list is palindrome:
“`haskell
isPalindrome :: Eq a => [a] -> Bool
isPalindrome xs = xs == reverse xs && length xs > 1
“`
In this example, the length function is used to check if the list has more than one element, which is necessary for it to be considered a palindrome.
FAQs
Q: What is the time complexity of the length function in Haskell?
A: The time complexity of the length function is O(n), where n is the number of elements in the input list.
Q: Is the length function implemented using recursion in Haskell?
A: Yes, the length function can be implemented using recursion in Haskell.
Q: What is the space complexity of the length function in Haskell?
A: The space complexity of the length function is also O(n), where n is the number of elements in the input list.
Q: Can the length function be used with lists of any data type?
A: Yes, the length function can be used with lists of any data type, as long as the type is an instance of the `Foldable` class.
Q: Are there any built-in list functions in Haskell that are similar to the length function?
A: Yes, Haskell provides other list manipulation functions such as `last`, `splitAt`, `chunksOf`, `elemIndex`, `delete`, and `null`, which can be used for various purposes.
Haskell For Imperative Programmers #4 – Lists And Tuples
Is There A Length Function In Haskell?
Haskell is a purely functional programming language that incorporates numerous powerful tools and features to simplify the process of developing robust and efficient programs. One key aspect of Haskell is its rich set of built-in functions, which enable programmers to perform a wide range of tasks with ease. The “length” function is a popular and frequently used function in many programming languages, so it is natural for Haskell developers to wonder if there is an equivalent function available in Haskell. In this article, we will explore the concept of the length function in Haskell and discuss its implementation and usage.
The length function, as the name suggests, calculates the number of elements in a given list or sequence. In most programming languages, this function is quite straightforward and easy to use. However, Haskell takes a different approach with its functional paradigm. Instead of a simple built-in function, Haskell provides a more powerful and generalized way to determine the length of a list.
In Haskell, the length function is not explicitly defined, but it can be derived using various methods. One common approach is to define a recursive function that iterates over the list and increments a counter until the end of the list is reached. Here’s an example implementation of the length function in Haskell:
“`
length’ :: [a] -> Int
length’ [] = 0
length’ (_:xs) = 1 + length’ xs
“`
In this implementation, the function `length’` takes a list (`[a]`) as input and returns an integer (`Int`). The function uses pattern matching to handle two cases. When an empty list is provided, the length is considered as 0. If the list has at least one element, the function recursively applies itself to the remaining part of the list (`xs`) and increments the counting variable by 1.
This recursive approach to calculating the length of a list reflects the fundamental principles of functional programming. Instead of directly performing a computation, Haskell creates a chain of recursive calls that gradually reduces the problem until a base case is reached. This approach allows for more concise and elegant code, but it also requires a good understanding of recursion.
Now that we have seen an example implementation of the length function in Haskell, let’s take a closer look at how it can be used in practice. One common use case is determining the length of a list before performing any further operations. For instance, imagine you have a list of elements and you want to verify if it meets certain length criteria. The length function can help you accomplish this easily. Here’s an example:
“`
checkLength :: [a] -> Bool
checkLength xs = length’ xs == 5
“`
In this example, the `checkLength` function takes a list as input and checks if its length is equal to 5 using the `length’` function we defined earlier. If the length is indeed 5, the function returns `True`; otherwise, it returns `False`. This simple example demonstrates how the length function can be leveraged to perform various length-related operations.
FAQs:
Q: Can the length function handle infinite lists?
A: No, the length function in Haskell cannot handle infinite lists. Since it relies on recursion to iterate through the list, it will never terminate when applied to an infinite list. To work with infinite lists, Haskell provides other techniques, such as laziness and infinite data structures like streams, which enable you to effectively manipulate and process potentially infinite data.
Q: Is the length function an efficient way to calculate the length of a list?
A: While the length function provides a straightforward way to get the length of a list, it has a time complexity of O(n), where n is the length of the list. This means that the function must traverse the entire list, resulting in linear time complexity. For practical purposes, it is generally more efficient to make use of different data structures or techniques that track the length information explicitly, such as vectors or finger trees.
Q: Can the length function handle lists with recursive structures?
A: Yes, the length function in Haskell can handle lists with recursive structures. Since it uses recursion to iterate through the list, it can handle any list structure, irrespective of whether it is recursive or not. The function will correctly count the number of elements in the list, regardless of its internal structure.
In conclusion, while Haskell does not provide a built-in length function like many other programming languages, it offers a powerful and flexible mechanism to calculate the length of lists. By leveraging recursion and pattern matching, Haskell developers can define their own length function and incorporate it into their programs. The length function in Haskell exemplifies the elegance and expressiveness of functional programming, while also demonstrating the scalability and extensibility of the language.
How Does Length Work In Haskell?
Haskell is a purely functional programming language, known for its elegant and concise code. One of the fundamental operations in many programming languages is computing the length of a list or an array. Haskell provides a built-in function called “length” that allows developers to determine the length of various data structures. In this article, we will explore how length works in Haskell and discuss its usage and some common queries.
Understanding the Basics:
The length function in Haskell is defined in the Prelude module, which is automatically imported in every Haskell program. It has the following type signature:
length :: [a] -> Int
The “length” function takes a list (denoted by “[a]”) and returns an integer (Int) representing the number of elements in that list. It is important to note that the computation of the length is not done iteratively; instead, Haskell’s lazy evaluation strategy ensures that elements are not actually counted until absolutely necessary.
For example, consider the following Haskell expression:
length [1, 2, 3, 4, 5]
When this expression is evaluated, it will return the integer 5, signifying the length of the list [1, 2, 3, 4, 5].
Handling Infinite Lists:
Haskell’s laziness and non-strict evaluation make it possible to work with infinite lists. However, calculating the length of an infinite list can pose a challenge, as it may result in an endless loop. The length function in Haskell handles this scenario gracefully by not attempting to evaluate an infinite list fully.
For instance, let’s consider the following expression:
length [1..]
Here, [1..] represents an infinite list starting from 1. In this case, Haskell does not get caught in an infinite loop when computing the length. Instead, it returns the result immediately, giving us an Integer value of “Infinity”.
Recursion and Length:
Haskell is a language that emphasizes recursion, and computing the length of a list is no exception. The length function itself is implemented using recursion in Haskell’s standard library. Let’s take a look at a simplified version of length’s implementation to get a better understanding:
length’ :: [a] -> Int
length’ [] = 0
length’ (x:xs) = 1 + length’ xs
Here, we define our own function called “length'” that takes a list as an argument. The first pattern `[]` matches an empty list and assigns a length of 0. When a non-empty list is supplied, the second pattern `(x:xs)` matches the head and tail of the list. We increment the length by 1 and recursively invoke the length’ function on the tail.
Using this recursive definition, we see how Haskell’s pattern matching and recursive capabilities work together to compute the length of a list.
Frequently Asked Questions:
Q: Can length be used with strings in Haskell?
A: Yes, definitely! In Haskell, strings are just lists of characters, so the length function can be directly applied to them. For example, the expression “length “Hello”” will return 5, as there are 5 characters in the string “Hello”.
Q: What happens when length is called on an empty list?
A: When the length function is invoked on an empty list (denoted by []), it returns 0. This aligns with the base case in our simplified implementation of length’ mentioned earlier.
Q: Is it possible to compute the length of a list without using the length function?
A: Yes, it is indeed possible to compute the length of a list without using the built-in length function. Developers can write their own recursive functions, similar to length’, to achieve the same result.
Q: Can length handle large lists efficiently?
A: Haskell uses lazy evaluation, which means that elements are not evaluated until absolutely necessary. This allows length to work efficiently on large lists, as it doesn’t evaluate the entire list, but rather computes the length as needed.
Q: Are there any limitations or edge cases to be aware of when using length in Haskell?
A: The length function in Haskell can handle most cases gracefully. However, it should be noted that computing the length of an infinite list will result in an infinite value (e.g., Infinity). Additionally, since the type signature of length returns an Int, its behavior may be unexpected when dealing with extremely large lists that exceed the capacity of Int.
In conclusion, Haskell provides a straightforward and efficient way to compute the length of lists using the built-in length function. With its lazy evaluation and recursive nature, Haskell ensures that length can handle both finite and infinite lists seamlessly. By understanding the concept and implementation of length, developers can leverage this functionality to better analyze and manipulate their data structures in Haskell applications.
Keywords searched by users: haskell length of list Length of list haskell, Take last element of list haskell, splitAt haskell, Chunksof haskell, Haskell find index of element in list, Split haskell, Haskell remove element from list, Null haskell
Categories: Top 26 Haskell Length Of List
See more here: nhanvietluanvan.com
Length Of List Haskell
Haskell, a widely-used functional programming language known for its strong static typing and lazy evaluation, offers powerful built-in functions and libraries that make it a favorite among developers. One of the fundamental operations frequently used in Haskell is determining the length of a list. In this article, we will delve into the intricacies of finding the length of a list in Haskell, discussing its implementation, performance, and common pitfalls.
Understanding the Implementation:
In Haskell, lists are defined using square brackets ([]), allowing you to create a sequence of elements of any type. The length of a list refers to the number of elements it contains. Haskell provides a built-in function called “length” to compute the length of a list. Here’s a simple example illustrating its usage:
“`haskell
main = do
let myList = [1, 2, 3, 4, 5]
print (length myList)
“`
The output of this code snippet will be 5, as the list “myList” contains five elements. The “length” function takes a list as its input and returns an integer representing the length of the list. This function can be used with any list, regardless of the type of its elements.
Performance Considerations:
When dealing with large lists, the performance of the “length” function becomes a significant concern. In Haskell, lists are implemented as linked lists, meaning the length computation involves iterating over each element, resulting in a time complexity of O(n), where n is the length of the list. As a result, finding the length of a large list can be noticeably slower than working with smaller lists.
It is crucial to note that lists in Haskell are lazy by default. This laziness means that only the necessary elements are evaluated, allowing for more efficient computations. However, when you apply the “length” function to an infinite list, it can lead to non-termination, as it will keep evaluating elements indefinitely. To handle such scenarios, Haskell provides a separate function called “genericLength” that works on infinite lists, but it returns an approximation instead of an exact length.
Common Pitfalls and Frequently Asked Questions:
1. Can I use the “length” function on an empty list?
Yes, the “length” function is perfectly capable of handling empty lists. When called on an empty list, it returns 0, indicating that there are no elements present.
2. Is there an alternative to “length” for computing the length of a list?
While “length” is the most straightforward approach, you can also write your custom recursive function to calculate the length of a list manually. However, it is generally advisable to use the built-in “length” function for simplicity and efficiency.
3. What happens if I try to find the length of an infinite list using “length”?
If you attempt to use the “length” function on an infinite list, it will not terminate and will keep evaluating elements indefinitely. To avoid such scenarios, consider using the “genericLength” function instead.
4. Are there any performance optimizations available for finding the length of a list?
Since the “length” function has a linear time complexity, there is no inherent optimization available. However, you can optimize your code by avoiding unnecessary operations or by using techniques like memoization to store previously computed lengths, reducing redundant computations.
Conclusion:
The length of a list is an essential metric when working with collections in Haskell. Regardless of the list’s size or type of its elements, Haskell provides the built-in “length” function to determine its length efficiently. However, it’s vital to consider the performance implications while dealing with large or infinite lists. Being aware of these nuances will enable you to write more efficient and reliable Haskell code.
Take Last Element Of List Haskell
Haskell is a functional programming language that provides a rich set of tools and functions to manipulate lists. One common operation when working with lists is to retrieve the last element. In Haskell, there are multiple ways to achieve this, each with its own advantages and trade-offs. In this article, we will explore various approaches to taking the last element of a list in Haskell, understand the differences between them, and provide examples to illustrate their functionality.
Methods for Taking the Last Element
Method 1: Using the last function
The most straightforward approach to take the last element of a list in Haskell is by using the built-in `last` function. This function takes a list as input and returns its last element.
“`haskell
lastElement :: [a] -> a
lastElement xs = last xs
“`
Using the `lastElement` function, we can easily retrieve the last element of any list. However, it is important to note that the `last` function can only be used with non-empty lists. If an empty list is passed as input, it will result in a runtime error. Therefore, it is crucial to ensure that the list is non-empty before using the `last` function.
Method 2: Using recursion
Another method to retrieve the last element of a list is by implementing a recursive function. This approach allows us to handle both non-empty and empty lists gracefully.
“`haskell
lastElementRec :: [a] -> Maybe a
lastElementRec [] = Nothing
lastElementRec [x] = Just x
lastElementRec (_:xs) = lastElementRec xs
“`
The `lastElementRec` function uses pattern matching to check the structure of the list. When an empty list is encountered, `Nothing` is returned, indicating that the list has no last element. If a list with a single element is passed, that element is returned using the `Just` constructor. For larger lists, the function recursively calls itself, passing the remainder of the list as the input.
This method gracefully handles empty lists, ensuring that the program doesn’t crash when attempting to retrieve the last element. It provides a more robust solution compared to the first method.
Method 3: Using a fold
Using a fold is another powerful and versatile way to extract the last element of a list in Haskell. By using the `foldl` function, we can accumulate values from left to right. However, since we are interested in the last element, we will utilize `foldl’` from the `Data.List` module, which is a stricter variant of `foldl` that reduces space usage and provides efficiency advantages.
“`haskell
import Data.List (foldl’)
lastElementFold :: [a] -> Maybe a
lastElementFold = foldl’ (\_ x -> Just x) Nothing
“`
The `lastElementFold` function uses `foldl’` and a lambda function to accumulate the elements of the list. Each element is ignored, while the last element is wrapped with `Just` by assigning it to the accumulator. Finally, the `Maybe` type is used as the return type to handle the possibility of an empty list.
This approach provides an elegant solution that doesn’t require explicit recursion and gracefully handles both empty and non-empty lists.
FAQs
Q: Can I use the `last` function with an empty list?
A: No, using the `last` function with an empty list will result in a runtime error. It is crucial to ensure that the list is non-empty before using the `last` function.
Q: How does the recursive approach handle empty lists?
A: The recursive approach gracefully handles empty lists by returning a `Nothing` value, indicating that the list has no last element.
Q: What is the advantage of using a fold to take the last element?
A: Using a fold provides an elegant and versatile solution that doesn’t require explicit recursion. It also gracefully handles empty and non-empty lists and offers performance benefits.
Q: Which method should I choose to take the last element of a list?
A: The choice of method depends on your specific requirements. If you are certain that the list is non-empty, you can use the `last` function. If you want a solution that handles empty lists gracefully, the recursive or fold-based approaches are more suitable.
Q: Are there any trade-offs when using the recursive approach?
A: The recursive approach is more robust in handling empty lists, but it may be slightly less efficient compared to the other methods due to the overhead of recursion. However, this performance difference is usually negligible for small to moderate-sized lists.
Conclusion
Taking the last element of a list is a common operation when working with Haskell. In this article, we explored three methods to achieve this: using the `last` function, implementing a recursive function, and employing a fold. Each method has its own advantages and trade-offs, and the choice depends on the specific requirements of your program. By understanding the various approaches and their functionality, you can confidently manipulate lists and retrieve the last element efficiently in Haskell.
Splitat Haskell
Haskell is a powerful functional programming language that offers a wide range of useful functions for data manipulation and processing. One such function is splitAt, which allows you to split a list into two parts at a specified index. In this article, we will explore the splitAt function in Haskell, discussing its syntax, functionality, and a variety of use cases.
Syntax and Functionality
The splitAt function is defined in the Data.List module of the Haskell standard library. Its syntax is as follows:
splitAt :: Int -> [a] -> ([a], [a])
The function takes two arguments: an integer representing the index at which to split the list, and the list itself. It returns a tuple containing two lists: the first list contains all elements up to the specified index, while the second list contains the remaining elements.
Let’s take a look at some examples to better understand the functionality of this function. Consider the following code snippet:
myList = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
result = splitAt 5 myList
In this example, we define a list called “myList” and then use the splitAt function to split the list at index 5. The resulting tuple, stored in the “result” variable, will contain two lists: [1, 2, 3, 4, 5] and [6, 7, 8, 9, 10].
The splitAt function is not limited to splitting the list at a specific index. Instead, it can handle various edge cases. For instance, splitting at index 0 will yield an empty list as the first element of the tuple, while the entire list remains as the second element. Splitting at the length of the list will have the opposite effect – the first element will contain the entire list, while the second element will be empty.
Functional Use Cases
The splitAt function is highly versatile and can be employed in a multitude of practical applications. Here are a few examples:
1. Pagination: When displaying a large dataset to users, pagination is crucial for efficient navigation. By using the splitAt function, you can split your dataset into pages, allowing users to view one page at a time.
2. Binary Trees: Splitting binary trees is a common operation in many algorithms and data structures. The splitAt function can be used to divide a binary tree into two subtrees, enabling further processing or analysis.
3. Parallel Processing: In scenarios where you need to distribute computational tasks across multiple processors, you can use the splitAt function to divide the workload evenly between them. Each processor can then work independently on its assigned subset of the data.
Frequently Asked Questions
Q: Can splitAt handle negative indices?
A: No, the splitAt function does not handle negative indices. If a negative value is provided, it will be treated as 0.
Q: Are the elements in the result tuple in the same order as the original list?
A: Yes, the order of the elements in the result tuple follows the order of the original list. The first list in the tuple contains elements up to the specified index, while the second list contains the remaining elements.
Q: Does splitAt modify the original list?
A: No, splitAt does not modify the original list. It returns a new tuple of lists, leaving the input list unchanged.
Q: What happens if the specified index is out of range?
A: If the specified index is beyond the bounds of the input list, splitAt will return a tuple with the entire list as the first element and an empty list as the second element.
Q: Can I split a string into two parts using splitAt?
A: Yes, splitAt can be used to split strings just like any other list in Haskell. Keep in mind that it operates on the list level, treating each character as a separate element.
Conclusion
The splitAt function in Haskell offers a simple yet powerful way to split lists at a specified index. Its versatility and ease of use make it a valuable tool for a wide range of functional programming tasks. By understanding the syntax, functionality, and possible use cases for splitAt, you can enhance your Haskell programming skills and employ this function to manipulate and process your data efficiently.
Images related to the topic haskell length of list

Found 24 images related to haskell length of list theme












.png)





Article link: haskell length of list.
Learn more about the topic haskell length of list.
- Haskell : length – ZVON.org
- length – Hoogle – Haskell.org
- The length of a list without the “length” function in Haskell
- How to find the length of a string in Haskell – Educative.io
- length – Hoogle – Haskell.org
- Starting Out – Learn You a Haskell for Great Good!
- What is takeWhile in Haskell? – Educative.io
- How to find the length of a string in Haskell – Educative.io
- Haskell – An Introduction – The Manchester Lambda Lounge
- Haskell Programming Tutorial: Recursive Functions on Lists
- Get list size, in Haskell – Programming Idioms
- Haskell Lists: The Ultimate Guide
- Lists – Haskell – DevTut
- Lists – Monday Morning Haskell