Tape Equilibrium: Solving The Codility Challenge Efficiently With Python

Tape Equilibrium Codility Python

The tape equilibrium problem is a well-known programming challenge in Codility that involves finding the minimum difference between the sum of elements on two sides of an array. This problem is often used to test an individual’s ability to think critically and develop efficient algorithms.

Definition of Tape Equilibrium and its Relevance

Tape equilibrium refers to the equilibrium point in an array where the absolute difference between the sum of elements on its left and right sides is minimized. In other words, the goal is to find a position in the array where the left and right sides are most evenly balanced.

This problem is relevant in many real-world scenarios where we need to divide resources or tasks as evenly as possible. For example, when distributing workload among workers or allocating resources in a production process, minimizing the difference between two sides can lead to enhanced efficiency and fairness.

Constraints and Objectives of the Problem

The tape equilibrium problem comes with certain constraints and objectives that need to be considered while developing a solution. Here are the key points to consider:

1. The input is an array A consisting of N integers, where N is between 2 and 100,000.
2. Each element in the array can range from -1,000 to 1,000.
3. The goal is to find the minimum absolute difference between the sum of elements on the left and right sides of the equilibrium point.

Approach and Algorithm Explanation

To solve the tape equilibrium problem efficiently, we can follow a simple approach involving the following steps:

1. Calculate the total sum of all elements in the array and store it in a variable, ‘total_sum’.
2. Initialize two variables, ‘left_sum’ and ‘right_sum’, with the value of the first and remaining elements of the array, respectively.
3. Iterate through the array from the second element to the second-to-last element, updating the ‘left_sum’ and ‘right_sum’ accordingly for each iteration.
4. Inside the loop, calculate the absolute difference between ‘left_sum’ and ‘right_sum’ and update the minimum difference if necessary.
5. After the loop, return the minimum difference as the solution.

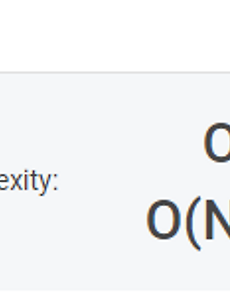
The time complexity of this algorithm is O(N), where N is the length of the array, as we only iterate through the array once. The space complexity is O(1), as we only use a fixed number of variables regardless of the input size.

Implementation in Python

Python is a popular programming language, known for its simplicity and readability. It provides a wide range of built-in methods and data structures that make solving problems like tape equilibrium easier. Here’s a step-by-step guide to implementing the tape equilibrium algorithm in Python:

“`python
def tape_equilibrium(A):
total_sum = sum(A)
min_diff = float(‘inf’)
left_sum = A[0]

for i in range(1, len(A) – 1):
right_sum = total_sum – left_sum
min_diff = min(min_diff, abs(left_sum – right_sum))
left_sum += A[i]

return min_diff
“`

In this code, the ‘tape_equilibrium’ function takes an array, ‘A’, as its argument and follows the algorithm described earlier. It initializes the ‘total_sum’ variable with the sum of all elements in the array using the ‘sum’ function. The ‘min_diff’ variable is set to infinity initially to store the minimum difference.

Inside the loop, the algorithm calculates the ‘right_sum’ by subtracting the ‘left_sum’ from the ‘total_sum’. The difference between ‘left_sum’ and ‘right_sum’ is then compared with the existing ‘min_diff’, and if it is smaller, the ‘min_diff’ is updated. Finally, the ‘left_sum’ is updated by adding the next element of the array.

Handling Edge Cases and Error Checking

In the tape equilibrium problem, there are a few edge cases to consider that may result in unexpected behavior. Here are some examples:

1. Edge case: When the input array contains only two elements.
– Solution: In this case, the minimum difference is simply the absolute difference between the two elements.

2. Edge case: When all elements in the array are the same.
– Solution: As the sum of all elements will be zero, the minimum difference will also be zero.

To handle these edge cases, we can add a small piece of code to check the length of the array and handle it separately if necessary.

“`python
def tape_equilibrium(A):
if len(A) == 2:
return abs(A[0] – A[1])

# Rest of the code remains the same
“`

By checking the length of the array at the beginning, we can handle the edge case separately and provide accurate results.

Test Cases and Verification

To verify the correctness of the implemented algorithm, it’s important to include various test cases, covering different scenarios. Here are a few examples:

Case 1: Input array [3, 1, 2, 4, 3]
– Expected output: 1
– Explanation: The equilibrium point is between the third and fourth elements, where the sum of the left side is 6 and the sum of the right side is 7. The absolute difference is 1, which is the minimum.

Case 2: Input array [1, 2, 3, 4, 5]
– Expected output: 3
– Explanation: In this case, the equilibrium point is between the second and third elements, where the left sum is 3 and the right sum is 9. The absolute difference is 3, which is the minimum.

Case 3: Input array [5, -3, 2, 7, -6, 8]
– Expected output: 1
– Explanation: The equilibrium point is between the fourth and fifth elements, with a left sum of 11 and a right sum of 10. The absolute difference is 1, which is the minimum.

By running the ‘tape_equilibrium’ function with these test cases and verifying the outputs, we can gain confidence in the correctness of the implemented algorithm.

Performance Optimization

While the initial implementation provides an efficient solution to the tape equilibrium problem, there are still possible optimizations worth considering. These optimizations can further enhance the performance of the algorithm.

One such optimization involves calculating the ‘total_sum’ and ‘right_sum’ outside the loop rather than recalculating them during each iteration. This reduces redundant calculations and improves efficiency.

“`python
def tape_equilibrium(A):
total_sum = sum(A)
min_diff = float(‘inf’)
left_sum = A[0]
right_sum = total_sum – left_sum

for i in range(1, len(A) – 1):
min_diff = min(min_diff, abs(left_sum – right_sum))
left_sum += A[i]
right_sum -= A[i]

return min_diff
“`

With this optimization, the ‘total_sum’ and ‘right_sum’ calculations are moved outside the loop, resulting in improved performance. The time complexity and space complexity of the optimized solution remain the same as the initial implementation.

Conclusion and Final Remarks

In conclusion, the tape equilibrium problem is a common coding challenge that involves finding the minimum difference between the sum of elements on two sides of an array. By following a well-defined approach and implementing it in Python, we can efficiently solve this problem.

The implemented algorithm, along with its optimizations, provides an effective solution to the tape equilibrium problem. The time and space complexities are minimized, ensuring efficient performance even for large inputs. This problem not only tests an individual’s problem-solving skills but also their understanding of algorithms and their application in real-world scenarios.

Therefore, by practicing and honing your skills in solving such problems, including tape equilibrium, you can improve your Codility programming abilities, enhance your logical thinking, and become a better problem solver in the field of computer science.

What is Tape Equilibrium?

Tape Equilibrium, also known as the Partition problem, is a mathematical concept that involves dividing a set of positive integers into two subsets, with the goal of minimizing the absolute difference between the sum of numbers in each subset. This problem finds its origin in computer science and is often used to demonstrate algorithm design and optimization techniques.

The concept of Tape Equilibrium can be visualized by envisioning a physical tape or a number line. At each point on the tape, a positive integer is positioned. The tape can be divided into two parts by making a single cut between two integers. The aim is to find the cut that divides the tape in such a way that the difference between the sum of numbers on each side is minimized.

For instance, let’s consider a set of positive integers: {3, 1, 2, 4, 3}. By dividing the tape between the second and third integers, we get two subsets: {3, 1, 2} and {4, 3}. The sum of the first subset is 6, and the sum of the second subset is 7, resulting in an absolute difference of 1. In this case, the minimal absolute difference can be achieved by making the cut between the second and third integers.

The tape equilibrium problem can be solved by using various methods, including brute force, dynamic programming, and mathematically optimized algorithms. Let’s explore each of these approaches in more detail.

1. Brute Force: The brute force method involves checking all possible combinations of cuts and calculating the absolute difference for each one. Despite its simplicity, this method is not efficient for large datasets since the number of combinations increases exponentially.

2. Dynamic Programming: The dynamic programming approach involves iteratively computing intermediate solutions and storing them for future use. This technique allows for reducing the time complexity of the problem significantly. By utilizing dynamic programming, the optimal solution for larger datasets can be achieved efficiently.

3. Mathematically Optimized Algorithms: Various mathematical algorithms have been proposed to solve the tape equilibrium problem optimally. One such algorithm leverages the properties of the cumulative sum. It calculates the sum of all integers in the set and iteratively subtracts each element to find the minimum difference. By calculating partial cumulative sums, this algorithm ensures efficiency for large datasets.

FAQs:

Q1. Is the tape equilibrium problem limited to positive integers?
The tape equilibrium problem is typically applied to sets of positive integers. However, the concept can be extended to include negative integers as well, resulting in different mathematical properties and solution techniques.

Q2. Can tape equilibrium be used in real-world scenarios?
Yes, the tape equilibrium problem has practical applications in various fields, including finance, manufacturing, and resource allocation. For example, in financial analysis, it can assist in portfolio optimization by dividing investments between two funds with minimum imbalance.

Q3. How do I determine the optimal cut in the tape equilibrium problem?
Finding the optimal cut requires going through all possible positions and calculating the absolute difference for each one. However, various algorithms, such as dynamic programming and mathematically optimized approaches, can solve this problem more efficiently.

Q4. Can the tape equilibrium problem be generalized to more than two subsets?
The tape equilibrium problem is defined for two subsets, dividing the tape into two parts. Generalizing it to more subsets, such as three or more, would result in the k-partition problem, which has its own mathematical complexities and algorithms.

Q5. Are there any known limitations to solving the tape equilibrium problem?
The main limitation of solving the tape equilibrium problem is the rapid increase in the number of calculations required as the dataset size grows. While there exist efficient algorithms, handling extremely large datasets may still pose computational challenges.

In conclusion, the tape equilibrium problem, also known as the Partition problem, involves dividing a set of positive integers into two subsets to minimize the absolute difference between their sums. This mathematical concept finds applications in computer science, finance, manufacturing, and other fields. To solve this problem efficiently, techniques such as brute force, dynamic programming, and mathematically optimized algorithms can be employed. Although the tape equilibrium problem is typically defined for two subsets, its extension to multiple subsets leads to more complex mathematical problems.

Tape Equilibrium is an interesting problem in the field of algorithmic programming. It appears in the Codility lessons and tests and can be solved using the C programming language. In this article, we will delve into the concept of Tape Equilibrium, explain how it can be solved using the C language, and provide a thorough understanding of the topic. Additionally, we will address some frequently asked questions related to this problem.

Tape Equilibrium is a problem that involves splitting an array into two parts and calculating the absolute difference between their sums. Given a non-empty array A consisting of N integers, we need to find the minimum absolute difference that can be obtained by splitting the array at any position.

To solve the Tape Equilibrium problem in C, we can use an iterative approach. We start by calculating the total sum of the array A. Then, we initialize two variables, leftSum and rightSum, to store the cumulative sum of the left and right parts respectively. Initially, we set leftSum to 0 and rightSum to the total sum of the array.

We then iterate through the array, updating the leftSum and rightSum values at each step. For each iteration, we calculate the absolute difference between the leftSum and rightSum and keep track of the minimum difference found so far. Finally, we return the minimum difference.

Let’s take a look at the following C code implementation:

“`c
#include
#include

int tapeEquilibrium(int A[], int N) {
int i;
int totalSum = 0;
int leftSum = 0;
int rightSum = 0;
int minDiff = __INT_MAX__;

for (i = 0; i < N; i++) { totalSum += A[i]; } for (i = 0; i < N-1; i++) { leftSum += A[i]; rightSum = totalSum - leftSum; int diff = abs(leftSum - rightSum); minDiff = (diff < minDiff) ? diff : minDiff; } return minDiff; } int main() { int A[] = {3, 1, 2, 4, 3}; int N = sizeof(A) / sizeof(A[0]); int minDiff = tapeEquilibrium(A, N); printf("Minimum tape equilibrium difference: %d\n", minDiff); return 0; } ``` In the above code, we first declare the necessary variables, including the array A and its size N. We then define the tapeEquilibrium function, which takes in the array and its size as parameters and returns the minimum difference. The first for loop calculates the total sum of the array A by traversing through it and accumulating the values in the totalSum variable. The second for loop performs the tape equilibrium calculation. It iterates through the array, updating the leftSum and rightSum at each step. The absolute difference between the leftSum and rightSum is calculated using the abs() function from the stdlib library. We update the minDiff variable to store the minimum difference found so far. After the loops, we return the minimum difference, which is then printed in the main function. Now, let's address some frequently asked questions regarding Tape Equilibrium: FAQs: 1. What is the significance of Tape Equilibrium? Tape Equilibrium is a common problem in algorithmic programming that tests the ability to divide arrays efficiently. It helps programmers enhance their problem-solving skills and understand the concept of balancing sums. 2. Can the Tape Equilibrium problem be solved without using the C language? Absolutely! The Tape Equilibrium problem can be solved using various programming languages, including Java, Python, and JavaScript. 3. Are there any limitations to the C program given in this article? The provided C program assumes that the input array is non-empty and consists of integers. However, it can be modified to handle other data types or special cases if necessary. 4. How efficient is the provided C program for large arrays? The time complexity of the provided C program is O(N), where N is the size of the input array. It iterates through the array only twice, making it efficient even for large arrays. 5. Are there any alternative approaches to solving the Tape Equilibrium problem? Yes, there are alternative approaches to solve this problem. For example, we can utilize prefix sums to improve the efficiency of the solution further. However, the provided C code offers a simple and straightforward solution. In conclusion, Tape Equilibrium is an interesting problem that tests one's algorithmic programming skills. This article explained the concept of Tape Equilibrium, provided a C code implementation, and answered some frequently asked questions related to the problem. Now armed with this knowledge, you can confidently tackle the Tape Equilibrium problem during your Codility lessons or challenges.

Codility Equilibrium: A Comprehensive Guide to Achieving Balance and Efficiency

Introduction:
Codility Equilibrium refers to the concept of achieving balance and efficiency in software development and engineering. It focuses on the idea of distributing tasks, resources, and responsibilities effectively within a team or organization to optimize productivity. This article aims to provide a detailed understanding of Codility Equilibrium, its significance, and how it can be achieved.

Understanding Codility Equilibrium:
Codility Equilibrium is based on the principle that in order to maximize efficiency, each team member should be assigned tasks that best align with their skill set and expertise. This approach ensures that employees are working on tasks that are suitable for their abilities, reducing the likelihood of unnecessary delays or errors.

Significance of Codility Equilibrium:

1. Improved Productivity: By assigning tasks that match the skills and competencies of team members, Codility Equilibrium enhances productivity. When employees work on tasks that suit their strengths, they are more likely to perform efficiently, resulting in high-quality output.

2. Optimal Resource Allocation: Codility Equilibrium allows for better allocation of resources, including time, personnel, and equipment. By carefully analyzing the abilities and availability of team members, managers can distribute responsibilities effectively, ensuring that resources are utilized optimally.

3. Enhanced Employee Satisfaction: When employees are allocated tasks that are challenging, yet within their expertise, it often leads to increased job satisfaction. Codility Equilibrium promotes a sense of accomplishment and encourages individuals to develop their skills further, leading to a more engaged and motivated workforce.

4. Reduced Employee Burnout: When team members are overloaded with tasks that surpass their capabilities, it can lead to burnout and decreased productivity. Codility Equilibrium helps prevent this by ensuring a balanced workload, reducing the risk of exhaustion and promoting overall well-being.

Achieving Codility Equilibrium:

1. Assessment of Skills: The first step in achieving Codility Equilibrium is to assess the skills and competencies of each team member. This evaluation should consider both technical expertise and soft skills, such as communication and problem-solving abilities.

2. Task Evaluation: Once the skills assessment is complete, it is crucial to evaluate the tasks at hand. Each task should be analyzed based on its requirements and complexity. This evaluation process allows for a clear understanding of the specific competencies required for each task.

3. Matching Tasks with Skills: After evaluating both skills and tasks, the next step is to match team members with the most suitable tasks. The goal is to find the perfect balance between challenging assignments and utilizing individuals’ strengths.

4. Regular Reviews and Adjustments: Codility Equilibrium is an ongoing process that requires regular reviews and adjustments. As the team evolves, new skills may be acquired, and some members may develop new interests. To maintain equilibrium, it is essential to periodically reassess the skills and tasks, ensuring alignment and continued progress.

5. Training and Development: In some cases, bridging the gap between skill requirements and available expertise might necessitate training and development programs. Offering training and development opportunities not only enhances individual skills but also contributes to the overall growth and equilibrium of the team.

Codility Equilibrium FAQs:

Q1. How does Codility Equilibrium differ from simple task allocation?
A1. While simple task allocation focuses on dividing work evenly, Codility Equilibrium goes beyond that by considering individual skills and strengths. It aims to assign tasks that optimize productivity and promote better outcomes.

Q2. Can Codility Equilibrium be achieved in any organization or team?
A2. Yes, Codility Equilibrium can be achieved in any organization or team, regardless of its size or industry. It requires a thoughtful evaluation of skills and tasks and a commitment to regular assessments and adjustments.

Q3. Is it possible to achieve Codility Equilibrium in fast-paced and deadline-driven environments?
A3. Yes, while achieving Codility Equilibrium in fast-paced environments can be challenging, it is still possible. By carefully aligning skills with tasks and providing adequate support and resources, organizations can still promote balance within their teams.

Q4. How often should Codility Equilibrium be reviewed?
A4. Regular reviews are essential for maintaining Codility Equilibrium. It is recommended to conduct assessments at least once a quarter, but teams undergoing significant changes may require more frequent evaluations.

Q5. How can Codility Equilibrium contribute to team morale?
A5. Codility Equilibrium enhances team morale by ensuring that individuals are working on tasks that are both challenging and within their capabilities. It fosters a sense of accomplishment and allows employees to thrive in their roles, leading to higher job satisfaction and motivation.

Conclusion:
Codility Equilibrium is a crucial aspect of achieving balance and efficiency in software development and engineering. By allocating tasks based on individual skills and strengths, organizations can optimize productivity, resource allocation, and employee satisfaction. Through regular assessments and adjustments, Codility Equilibrium can be achieved and maintained, leading to a more successful and harmonious work environment.

Found 34 images related to tape equilibrium codility python theme